
【题目】如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=﹣x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 . 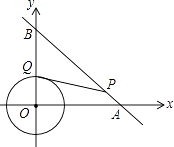
【答案】2
【解析】解:连结OP,OQ,作OH⊥AB于H,如图,
当x=0时,y=﹣x+4=4,则B(0,4);当y=0时,﹣x+4=0,解得x=4,则A(4,0),
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB= ![]() OA=4
OA=4 ![]() ,
,
∵OH⊥AB,
∴OH= ![]() AB=2
AB=2 ![]() ,
,
∵PQ为⊙O的切线,
∴OQ⊥PQ,
在Rt△POQ中,PQ= ![]() =
= ![]() ,
,
∴当OP最小时,PQ最小,
而OP=OH时,OP最小,
∴切线长PQ的最小值= ![]() =2,
=2,
所以答案是:2.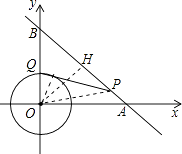
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).


科目:初中数学 来源: 题型:
【题目】新世纪广场进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市后果然供不应求,商场又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了4元,商场销售这种衬衫时每件定价都是58元,最后剩下的150件按八折销售,很快售完,在这两笔生意中,商场共赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标是(-5,0),(-4,-2),(-3,0),(-2,-2),(-1,0)的点用线段依次连接起来形成一个图案Ⅰ.
(1)作出该图案关于y轴对称的图案Ⅱ;
(2)将所得到的图案Ⅱ沿x轴向上翻折180°后得到一个新图案Ⅲ,试写出它的各顶点的坐标;
(3)观察图案Ⅰ与图案Ⅲ,比较各顶点的坐标和图案位置,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
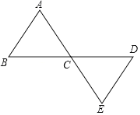
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
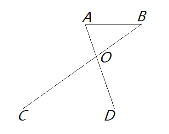
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com