
ЁОЬтФПЁПЮЊСЫСЫНтФГбЇаЃЦпФъМЖ4ИіАрЙВ180ШЫЕФЬхжЪНЁПЕЧщПіЃЌДгИїАрЗжБ№ГщШЁЭЌбљЪ§СПЕФФаЩњКЭХЎЩњзщГЩвЛИібљБОЃЌАбЬхжЪЧщПіСПЛЏЕУЗжЃЌЙцЖЈЕУЗжxТњзуxЃМ60ЮЊВЛМАИёЃЌ60ЁмxЃМ80ЮЊМАИёЃЌ80ЁмxЃМ90ЮЊСМКУЃЌЁн90ЮЊгХауЃЌЯТЭМЪЧИљОнбљБОЪ§ОнЛцжЦЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ
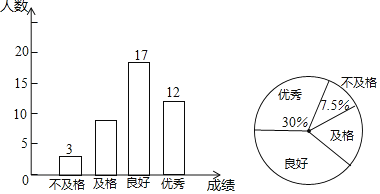
ЃЈ1ЃЉБОДЮГщВщЕФбљБОШнСПЪЧ
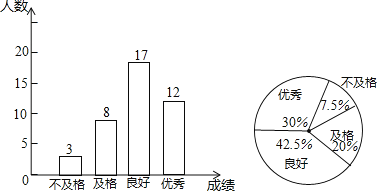
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭМЩЯЕФЪ§зжКЭЩШаЮЭМжаЕФАйЗжЪ§ЃЎ
ЃЈ3ЃЉЧыФуЙРМЦШЋаЃЦпФъМЖЕУЗжВЛЕЭгк90ЗжЕФдМгаЖрЩйШЫЃЎ
ЁОД№АИЁПЃЈ1ЃЉ40ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ54ЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУВЛМАИёШЫЪ§Г§вдВЛМАИёШЫЪ§ЫљеМАйЗжБШПЩЕУГщВщЕФбљБОШнСПЃЛ
ЃЈ2ЃЉРћгУЬѕаЮЭММЦЫуГіМАИёШЫЪ§ЃЌдйИљОнбљБОШнСПМЦЫуГіМАИёШЫЪ§КЭСМКУШЫЪ§ЫљеМАйЗжБШМДПЩЃЛ
ЃЈ3ЃЉРћгУбљБОЙРМЦзмЬхЕФЗНЗЈгУ180ГЫвдбљБОжаЕУЗжВЛЕЭгк90ЗжЕФШЫЪ§ЫљеМАйЗжБШПЩЕУД№АИЃЎ
НтЃКЃЈ1ЃЉ3ЁТ7.5%=40ЃЌ
ЙЪД№АИЮЊЃК40ЃЛ
ЃЈ2ЃЉМАИёШЫЪ§40-3-17-12=8ЃЌ
МАИёЫљеМАйЗжБШЃК8ЁТ40ЁС100%=20%ЃЌ
СМКУЫљеМАйЗжБШЃК17ЁТ40ЁС100%=42.5%ЃЛ
ЃЈ3ЃЉ180ЁС30%=54ЃЈШЫЃЉЃЌ
Д№ЃКЙРМЦШЋаЃЦпФъМЖЕУЗжВЛЕЭгк90ЗжЕФдМга54ШЫЃЎ


 УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§СНЕуAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌЧвЦфЖдГЦжсЮЊжБЯпxЃНЉ1ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧХзЮяЯпЩЯЕуAгыЕуBжЎМфЕФЖЏЕуЃЈВЛАќРЈЕуAЃЌЕуBЃЉЃЌЧѓЁїPABЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкАыдВЃЌABЮЊжБОЖЃЌЙ§ЕуAзїжБЯпMNЃЌШєЁЯMAC=ЁЯABCЃЎ

ЃЈ1ЃЉЧѓжЄЃКMNЪЧАыдВЕФЧаЯпЃЎ
ЃЈ2ЃЉЩшDЪЧЛЁACЕФжаЕуЃЌСЌНгBDНЛACгкGЃЌЙ§DзїDEЁЭABгкEЃЌНЛACгкFЃЌЧѓжЄЃКFD=FGЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЕФЪЧХзЮяЯпаЭЙАЧХЃЌЕБЙАЖЅРыЫЎУц2mЪБЃЌЫЎУцПэ4mЃЌШєЫЎУцЯТНЕ2mЃЌдђЫЎУцПэЖШдіМгЃЈ ЃЉ
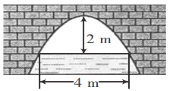
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCOЮЊОиаЮЃЌЕуAдкxжсЩЯЃЌЕуCдкyжсЩЯЃЌЧвЕуBЕФзјБъЮЊЃЈ2,1ЃЉЃЌНЋДЫОиаЮШЦЕуOФцЪБеыа§зЊ90ЁуЕУОиаЮDEFOЃЌХзЮяЯпy=-x2+bx+cЙ§BЁЂEСНЕу.
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФКЏЪ§НтЮіЪН.
ЃЈ2ЃЉНЋОиаЮDEFOЯђгвЦНвЦЃЌЕБЕуEЕФЖдгІЕуEЁЏдкХзЮяЯпЩЯЪБЃЌЧѓЯпЖЮDFЩЈЙ§ЕФУцЛ§.
ЃЈ3ЃЉШєНЋОиаЮABCOЯђЩЯЦНвЦdИіЕЅЮЛГЄЖШКѓЃЌФмЪЙДЫХзЮяЯпЕФЖЅЕудкДЫОиаЮЕФБпЩЯЃЌЧѓdЕФжЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
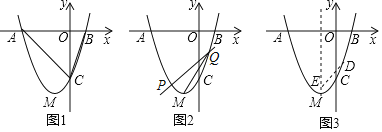
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=ax2+2ax+cгыxжсНЛгкAЃЈ-3ЃЌ0ЃЉЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЁїABCЕФУцЛ§ЮЊ6ЃЌХзЮяЯпЖЅЕуЮЊMЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпy=kx+k-3гыХзЮяЯпНЛгкPЁЂQСНЕуЃЈPЕудкQЕузѓВрЃЉЃЌЮЪдкyжсЩЯЪЧЗёДцдкЕуNЃЌЪЙЫФБпаЮPMQNЮЊОиаЮЃПШєДцдкЃЌЧѓNЕузјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєDЮЊХзЮяЯпЩЯШЮвтвЛЕуЃЌEЃЈ-1ЃЌsЃЉЮЊЖдГЦжсЩЯвЛЕуЃЌШєЖдШЮвтвЛЕуDЖМгаEDЁнEMЃЌЧѓsЕФзюДѓжЕМАЯргІEЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКьЪїСжбЇаЃдкЦпФъМЖаТЩњжаОйааСЫШЋдБВЮМгЕФЁАЗРФчЫЎЁБАВШЋжЊЪЖОКШќЃЌЪдОэЬтФПЙВ10ЬтЃЌУПЬт10ЗжЃЎЯжЗжБ№ДгШ§ИіАржаИїЫцЛњШЁ10УћЭЌбЇЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЃЌЪеМЏЪ§ОнШчЯТЃК
1АрЃК90ЃЌ70ЃЌ80ЃЌ80ЃЌ80ЃЌ80ЃЌ80ЃЌ90ЃЌ80ЃЌ100ЃЛ
2АрЃК70ЃЌ80ЃЌ80ЃЌ80ЃЌ60ЃЌ90ЃЌ90ЃЌ90ЃЌ100ЃЌ90ЃЛ
3АрЃК90ЃЌ60ЃЌ70ЃЌ80ЃЌ80ЃЌ80ЃЌ80ЃЌ90ЃЌ100ЃЌ100ЃЎ
ећРэЪ§ОнЃК
ЗжЪ§ ШЫЪ§ АрМЖ | 60 | 70 | 80 | 90 | 100 |
1Ар | 0 | 1 | 6 | 2 | 1 |
2Ар | 1 | 1 | 3 |
| 1 |
3Ар | 1 | 1 | 4 | 2 | 2 |
ЗжЮіЪ§ОнЃК
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | |
1Ар | 83 | 80 | 80 |
2Ар | 83 |
|
|
3Ар |
| 80 | 80 |
ИљОнвдЩЯаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыжБНгаДГіБэИёжа![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉБШНЯетШ§зщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§КЭжкЪ§ЃЌФуШЯЮЊФФИіАрЕФГЩМЈБШНЯКУЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЮЊСЫШУбЇЩњжиЪгАВШЋжЊЪЖЕФбЇЯАЃЌбЇаЃНЋИјОКШќГЩМЈТњЗжЕФЭЌбЇАфЗЂНБзДЃЌИУаЃЦпФъМЖаТЩњЙВ570ШЫЃЌЪдЙРМЦашвЊзМБИЖрЩйеХНБзДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЃЌCDЪЧдВOЕФжБОЖЃЌAEЪЧдВOЕФЯвЃЌЧвAEЁЮCDЃЌЙ§ЕуCЕФдВOЧаЯпгыEAЕФбгГЄЯпНЛгкЕуPЃЌСЌНгACЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЦНЗжЁЯBAPЃЛ
ЃЈ2ЃЉЧѓжЄЃКPC2=PAPEЃЛ
ЃЈ3ЃЉШєAE-AP=PC=4ЃЌЧѓдВOЕФАыОЖЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬсГіЃК
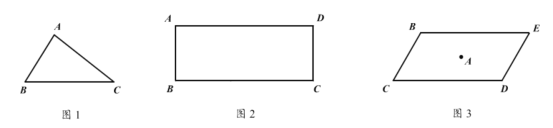
ЃЈ1ЃЉШчЭМ1ЃЌвбжЊЁїABCЃЌЪдШЗЖЈвЛЕуDЃЌЪЙЕУвдAЃЌBЃЌCЃЌDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧыЛГіетИіЦНааЫФБпаЮЃЛ
ЮЪЬтЬНОПЃК
ЃЈ2ЃЉШчЭМ2ЃЌдкОиаЮABCDжаЃЌAB=4ЃЌBC=10ЃЌШєвЊдкИУОиаЮжазїГівЛИіУцЛ§зюДѓЕФЁїBPCЃЌЧвЪЙЁЯBPCЃН90ЁуЃЌЧѓТњзуЬѕМўЕФЕуPЕНЕуAЕФОрРыЃЛ
ЮЪЬтНтОіЃК
ЃЈ3ЃЉШчЭМ3ЃЌгавЛзљВнИљЫўAЃЌАДЙцЖЈЃЌвЊвдЫўAЮЊЖдГЦжааФЃЌНЈвЛИіУцЛ§ОЁПЩФмДѓЕФаЮзДЮЊЦНааЫФБпаЮЕФВнИљОАЧјBCDEЁЃИљОнЪЕМЪЧщПіЃЌвЊЧѓЖЅЕуBЪЧЖЈЕуЃЌЕуBЕНЫўAЕФОрРыЮЊ50УзЃЌЁЯCBE=120ЁуЃЌФЧУДЃЌЪЧЗёПЩвдНЈвЛИіТњзувЊЧѓЕФУцЛ§зюДѓЕФЦНааЫФБпаЮОАЧјBCDEЃПШєПЩвдЃЌЧѓГіТњзувЊЧѓЕФЦНааЫФБпаЮBCDEЕФзюДѓУцЛ§ЃЛШєВЛПЩвдЃЌЧыЫЕУїРэгЩЁЃЃЈЫўAЕФеМЕиУцЛ§КіТдВЛМЦЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com