
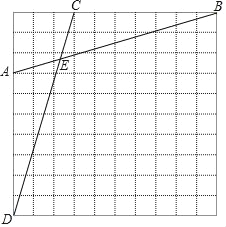
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,AB与CD相交于点E.
(Ⅰ)AB的长等于 ;
(Ⅱ)点F是线段DE的中点,在线段BF上有一点P,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(Ⅰ)利用勾股定理计算即可;
(Ⅱ)连接AC、BD.易知:AC∥BD,可得:EC:ED=AC:BD=3:10,取格点G、H,连接GH交DE于F,因为DG∥CH,所以FD:FC=DG:CH=5:8,可得DF=EF.取格点I、J,连接IJ交BD于K,因为BI∥DJ,所以BK:DK=BI:DJ=5:6,连接EK交BF于P,可证BP:PF=5:3;
详解:(Ⅰ)AB的长=![]() =
=![]() ;
;
(Ⅱ)由题意:连接AC、BD.易知:AC∥BD,
可得:EC:ED=AC:BD=3:10.
取格点G、H,连接GH交DE于F.
∵DG∥CH,∴FD:FC=DG:CH=5:8,可得DF=EF.
取格点I、J,连接IJ交BD于K.
∵BI∥DJ,∴BK:DK=BI:DJ=5:6.
连接EK交BF于P,可证BP:PF=5:3.

故答案为:(Ⅰ)![]() ;
;
(Ⅱ)由题意:连接AC、BD.
易知:AC∥BD,可得:EC:ED=AC:BD=3:10,
取格点G、H,连接GH交DE于F.
因为DG∥CH,所以FD:FC=DG:CH=5:8,可得DF=EF.
取格点I、J,连接IJ交BD于K.
因为BI∥DJ,所以BK:DK=BI:DJ=5:6,
连接EK交BF于P,可证BP:PF=5:3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
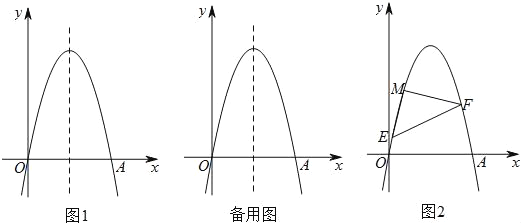
【题目】如图1,抛物线y=﹣x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.
(1)这条抛物线的对称轴是:直线 ,直线PQ与x轴所夹锐角的度数是 度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在平面直角坐标系中,A(![]() ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=![]() .
.

(1)求直线AD的解析式和线段BD所在直线的解析式.
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:四边形
,求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,当
,当![]() 时,取
时,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形
,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目:初中数学 来源: 题型:
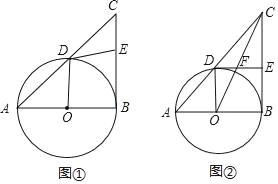
【题目】Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com