练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （7分）阅读材料，解答问题：
    命题：如图，在锐角△ABC中，BC=a,CA=b,AB=c,ΔABC的外接圆半径为R，
    则2R.

    证明:连结CO并延长交⊙O于点D，连结DB，则∠D＝∠A，因为CD是⊙O的直径，所以∠DBC＝900，在Rt△DBC中，sinD=,所以sinA=,即，同理：,   ∴ 2R.
    请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
    小题1:（1）前面阅读材料中省略了“”的证明过程，请你把“”的证明过程补写出来.
    小题2:（2）直接运用阅读材料中命题的结论解题：已知锐角△ABC中， BC＝，CA＝，∠A＝600，求△ABC的外接圆半径 R及∠C.

    小题1:略
    小题2:1,75°
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：计算题

    求式子的值：

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

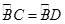    已知：如图，⊙O的直径AB与弦CD相交于Ｅ，， BF⊥AB与弦AD的延长线相交于点F．

    小题1:（1）求证：CD∥BF；
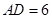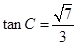    小题2:（2）连结BC，若，，求⊙O的半径 及弦CD的长．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    △ABC中，∠C＝90°，sinA＝，则tanB的值为(    )
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    在中，，则

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题满分8分）
    如图，河岸边有座水塔AB，测量人员在河对岸C处测得塔顶A的仰角为300，然后沿着CB方向前进30米到达D处，又测得A的仰角为450，请根据上述数据计算水塔的高(结果精确到0.1)（）.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    (8分)在东西方向的海岸线上有一长为1km的码头MN（如图），在码头西端M 的正西19．5 km 处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距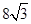km的C处．

    小题1:（1）求该轮船航行的速度（保留精确结果）；
    小题2:（2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：计算题

    （本题满分10分）
    计算：．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

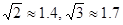    如图，河两岸a，b互相平行，C，D是河岸a上间隔40米的两根电线杆，某人在河岸b上的A处，测得∠DAE=45°，然后沿河岸走了30米到达B处，测得∠CBE=60°，求河的宽度（结果精确到1米，）．

    查看答案和解析>>

    同步练习册答案