
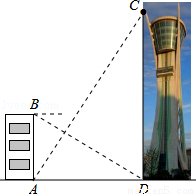
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016届浙江省绍兴市九年级下学期3月月考数学试卷(解析版) 题型:填空题
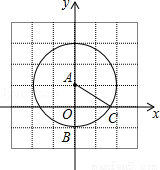
如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于 度.
查看答案和解析>>
科目:初中数学 来源:2016届天津一中九年级上学期第二次月考数学试卷(解析版) 题型:解答题
如图,△ABC中,CD是边AB上的高,且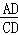 =
=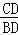 .
.
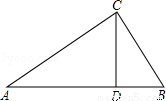
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
查看答案和解析>>
科目:初中数学 来源:2016届天津一中九年级上学期第二次月考数学试卷(解析版) 题型:选择题
圆的周长是2π,如果一条直线与圆心的距离是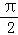 ,那么这条直线与这个圆的位置关系是( )
,那么这条直线与这个圆的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2016届山东省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为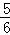 m.
m.
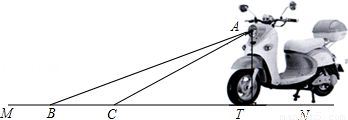
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是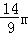 ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈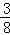 ,tan22°≈
,tan22°≈ ,sin31°≈
,sin31°≈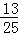 ,tan31°≈
,tan31°≈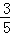 )
)
查看答案和解析>>
科目:初中数学 来源:2016届山东省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,CD=3,AB=4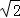 ,则⊙O的直径等于( )
,则⊙O的直径等于( )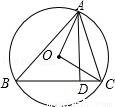
A.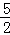
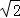 B.3
B.3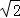 C.5
C.5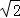 D.7
D.7
查看答案和解析>>
科目:初中数学 来源:2016届山东省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
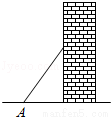
A.sinA的值越大,梯子越陡
B.cosA的值越大,梯子越陡
C.tanA的值越小,梯子越陡
D.陡缓程度与∠A的函数值无关
查看答案和解析>>
科目:初中数学 来源:2016届山东省泰安市东平县九年级上学期期中数学试卷(解析版) 题型:选择题
如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )
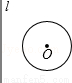
A.1cm B.2cm C.4cm D.2cm或4cm
查看答案和解析>>
科目:初中数学 来源:2016届山东省九年级上学期10月月考数学试卷(解析版) 题型:解答题
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
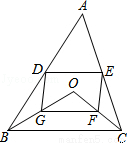
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?为什么?
(3)当OA与BC满足 时,四边形DGEF是一个矩形(直接填答案,不需证明.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com