
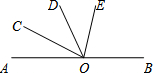
 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )| A. | 360°-4α | B. | 180°-4α | C. | α | D. | 2α-60° |
分析 设∠DOE=x,则∠BOE=2x,根据角之间的等量关系求出∠AOD、∠COD、∠COE的大小,然后解得x即可.
解答 解:设∠DOE=x,则∠BOE=2x,
∵∠BOD=∠BOE+∠EOD,
∴∠BOD=3x,
∴∠AOD=180°-∠BOD=180°-3x.
∵OC平分∠AOD,
∴∠COD=$\frac{1}{2}$∠AOD=$\frac{1}{2}$(180°-3x)=90°-$\frac{3}{2}$x.
∵∠COE=∠COD+∠DOE=90°-$\frac{3}{2}$x+x=90°-$\frac{x}{2}$,
由题意有90°-$\frac{x}{2}$=α,解得x=180°-2α,即∠DOE=180°-2α,
∴∠BOE=360°-4α,
故选:A.
点评 本题主要考查角的计算的知识点,运用好角的平分线这一知识点是解答的关键,本题难度不大.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | y1=y2>y3 | B. | y1=y3<y2 | C. | y1=y3=y2 | D. | y1>y2>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
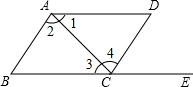 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
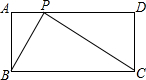 如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.
如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com