
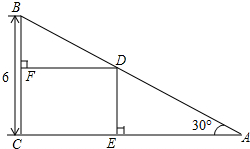
 王师傅想在一块三角形剩料中挖去一块最大矩形料做其他用途,其图形和数据如图所示,请你计算王师傅所取得最大矩形料的面积是9$\sqrt{3}$,这时CE=3,CF=3$\sqrt{3}$.
王师傅想在一块三角形剩料中挖去一块最大矩形料做其他用途,其图形和数据如图所示,请你计算王师傅所取得最大矩形料的面积是9$\sqrt{3}$,这时CE=3,CF=3$\sqrt{3}$. 分析 先根据锐角三角函数的定义求出AC的长,再设CE=a,CF=b,则BF=6-b,AE=AC-b,再由矩形的面积公式可得出结论.
解答 解:∵BC=6,∠A=30°,
∴AC=$\frac{6}{tan30°}$=6$\sqrt{3}$.
设CE=a,CF=b,则BF=6-b,AE=6$\sqrt{3}$-b,
∵DF∥AC,DE∥BC,
∴△BDF∽△BAC,
∴$\frac{DF}{AC}$=$\frac{BF}{BC}$,即$\frac{a}{6\sqrt{3}}$=$\frac{6-b}{6}$,
∴a=6$\sqrt{3}$-$\sqrt{3}$b,
∴S=ab=(6$\sqrt{3}$-$\sqrt{3}$b)b=-$\sqrt{3}$b2+6$\sqrt{3}$b,
∴当b=$\frac{6\sqrt{3}}{2\sqrt{3}}$=3时,S最大=$\frac{-(6\sqrt{3})^{2}}{-4\sqrt{3}}$=9$\sqrt{3}$,
∴此时a=6$\sqrt{3}$-3$\sqrt{3}$=3$\sqrt{3}$,
∴最大矩形料的面积是9$\sqrt{3}$,此时CE=3,CF=3$\sqrt{3}$.
故答案为:9$\sqrt{3}$,3,3$\sqrt{3}$.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
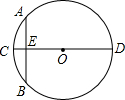 “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
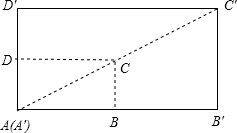 如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
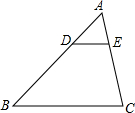 如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:
如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
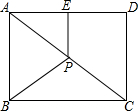 如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )| A. | 14 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com