
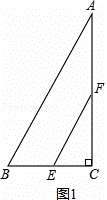
如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,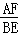 = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
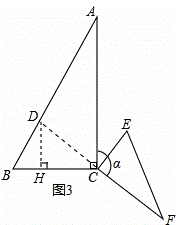
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2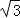 ,求旋转角a的度数.
,求旋转角a的度数.
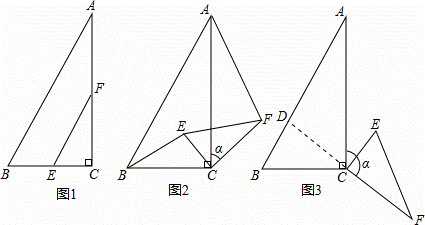
解:(1)如图1,线段BE与AF的位置关系是互相垂直;
∵∠ACB=90°,BC=2,∠A=30°,
∴AC=2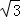 ,
,
∵点E,F分别是线段BC,AC的中点,
∴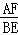 =
=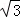 ;
;
故答案为:互相垂直;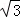 ;
;
(2)(1)中结论仍然成立.
证明:如图2,∵点E,F分别是线段BC,AC的中点,
∴EC=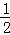 BC,FC=
BC,FC=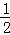 AC,
AC,
∴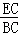 =
=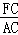 =
=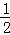 ,
,
∵∠BCE=∠ACF=α,
∴△BEC∽△AFC,
∴ =
=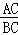 =
=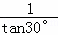 =
=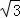 ,
,
∴∠1=∠2,
延长BE交AC于点O,交AF于点M
∵∠BOC=∠AOM,∠1=∠2
∴∠BCO=∠AMO=90°
∴BE⊥AF;
(3)如图3,∵∠ACB=90°,BC=2,∠A=30°
∴AB=4,∠B=60°
过点D作DH⊥BC于H
∴DB=4﹣(6﹣2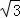 )=2
)=2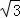 ﹣2,
﹣2,
∴BH=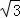 ﹣1,DH=3﹣
﹣1,DH=3﹣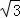 ,
,
又∵CH=2﹣(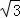 ﹣1)=3﹣
﹣1)=3﹣ ,
,
∴CH=DH,
∴∠HCD=45°,
∴∠DCA=45°,
∴α=180°﹣45°=135°.



科目:初中数学 来源: 题型:
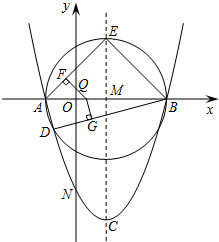
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,﹣4),与x轴交于A、B两点,与y轴交于点N(0,﹣3).
(1)求这条抛物线的解析式;
(2)如图,以AB为直径作⊙M,与抛物线交于点D,与抛物线的对称轴交于点E,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作QF⊥AE于F,QG⊥DB于G,请判断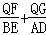 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;
(3)请求出抛物线与(2)中⊙M的所有交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
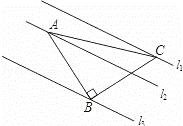
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( )
A. 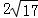 B.
B. 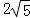 C.
C. 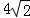 D. 7
D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
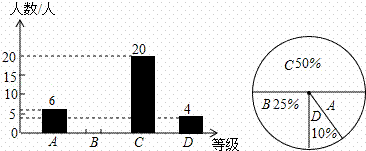
为了解本校2015年九年级学生期末数学考试情况,小明在九年 级随机抽取了一部分学生的期末数学成绩为样本,分为A(85分或85分以上)、B(84~70分)、C(69~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如图统计图,请你根据统计图解答以下问题:
(1)这次随机抽取的学生共有多少人?
请补全条形统计图;
(3)这个学校2015年九年级共有学生600人,估计这次2015年九年级学生期末数学考试成绩为A等级的学生人数大约有多少?扇形统计图中A等级的圆心角多少度?
(4)随机抽取一个学生了解成绩,抽到A等级的学生的概率约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com