【题目】已知ABCD的周长为26，∠ABC=120°，BD为一条对角线，⊙O内切于△ABD，E，F，G为切点，已知⊙O的半径为
．求ABCD的面积．
【答案】20
【解析】
首先利用三边及⊙O的半径表示出平行四边形的面积，再根据题意求出AB+AD=13，然后利用切线的性质求出BD的长即可解答.
设⊙O分别切△ABD的边AD、AB、BD于点G、E、F；
平行四边形ABCD的面积为S；
则S=2S△ABD=2×
(AB·OE+BD·OF+AD·OG)=（AB+AD+BD）；
∵平行四边形ABCD的周长为26，
∴AB+AD=13，
∴S=(13+BD)；连接OA；
由题意得：∠OAE=30°，
∴AG=AE=3；同理可证DF=DG，BF=BE；
∴DF+BF=DG+BE=13﹣3﹣3=7，
即BD=7，
∴S=（13+7）=20．
即平行四边形ABCD的面积为20．
科目：初中数学 来源： 题型：
【题目】某通讯公司推出①，②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示．
(1)有月租的收费方式是________(填“①”或“②”)，月租费是________元；
(2)分别求出①，②两种收费方式中y与自变量x之间的函数表达式；
(3)请你根据用户通讯时间的多少，给出经济实惠的选择建议．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，D、E分别在BC、AC上，且CD=AE，AD与BE相交于P，BQ⊥AD于Q.
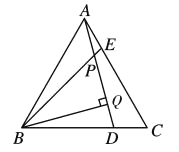
（1）求证：
；
（2）若PQ=4，PE=1，求AD的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c（0＜2a＜b）的顶点为P（x0，y0），点A（1，yA），B（0，yB），C（﹣1，yC）在该抛物线上，当y0≥0恒成立时，
的最小值为（ ）
A. 1 B. 2 C. 4 D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，∠DAB=∠ABC=90°，AB=BC，E是AB的中点，CE⊥BD．
（1）求证：BE=AD；
（2）求证：AC是线段ED的垂直平分线；
（3）△DBC是等腰三角形吗？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用一条24cm的细绳围成一个等腰三角形。
（1）如果腰长是底边的2倍，那么各边的长是多少？
（2）能围成有一边长为4cm的等腰三角形吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
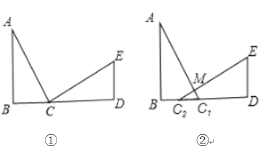
（1）求证：△ABC≌△CDE
（2）试判断AC与CE的位置关系，并说明理由．
（3）若将CD沿CB方向平移得到图②的情形，其余条件不变，此时第（2）问中AC与CE的位置关系还成立吗？请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点
若点D为BC边的中点，点M为线段EF上一动点，则
周长的最小值为
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC的边长为8，AD是BC边上的中线，点E是AC边上的一点，AE=2，若点M是线段AD上的一个动点，则ME+MC的最小值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com