
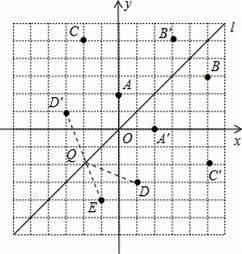
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′ 、C′ ;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为 (不必证明);
运用与拓广:
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.


【考点】一次函数综合题.
【专题】综合题.
【分析】易找到点B关于第一、三象限角平分线的对称点B′的坐标为(3,5),再结合已知的点A的坐标,我们不难猜想点C′坐标是(5,﹣2),然后找到点C′,可以发现CC′被第一、三象限角平分线垂直且平分,由此可以推想到坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a),即它们纵、横坐标互换位置.
【解答】解:(1)如图:B′(3,5),C′(5,﹣2);
(2)(b,a);
(3)由(2)得,D(1,﹣3)关于直线l的对称点D′的坐标为(﹣3,1),连接D′E交直线l于点Q,此时点Q到D、E两点的距离之和最小.
设过D′(﹣3,1)、E(﹣1,﹣4)直线的解析式为y=kx+b,
则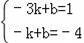

∴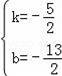

∴直线D′E的解析式为:y=﹣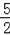
 x﹣
x﹣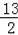

由

得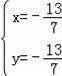

∴所求Q点的坐标为(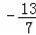
 ,
,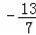
 ).
).

【点评】本题的解答经历了实验﹣﹣猜想﹣﹣验证﹣﹣推广的思维过程,这也是我们认识事物规律的一般方法,主要考查一次函数的性质和图象,中等难度.


科目:初中数学 来源: 题型:
一名射击运动员连续射靶10次,其中2次命中10环,2次命中9环 ,6次命中8环.则下列说法正确的是 ( )
,6次命中8环.则下列说法正确的是 ( )
A.命中环数的平均数是9 B.命中环数的中位数是9
C.命中环数的众数是10 D.命中环数的众数和中位数是8[来源:Z#xx#k.Com]
查看答案和解析>>
科目:初中数学 来源: 题型:
商店某天销售了11件衬衫,其领口尺寸统计如下表:
| 领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
| 件数 | 1 | 4 | 3 | 1 | 2 |
则这ll件衬衫领口尺寸的众数是________cm,中位数是________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;

(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为 稳定.
稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列条件之一能使菱形ABCD是正方形的为( )

①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD.
A.①③ B.②③ C.②④ D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com