
 如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.分析 (1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值,进而可用配方法求出其顶点D的坐标;
(2)根据抛物线的解析式可求出C点的坐标,由于CD是定长,若△CDH的周长最小,那么CH+DH的值最小,由于EF垂直平分线段BC,那么B、C关于直线EF对称,所以BD与EF的交点即为所求的H点;易求得直线BC的解析式,关键是求出直线EF的解析式;由于E是BC的中点,根据B、C的坐标即可求出E点的坐标;可证△CEG∽△COB,根据相似三角形所得的比例线段即可求出CG、OG的长,由此可求出G点坐标,进而可用待定系数法求出直线EF的解析式,由此得解;
(3)过K作x轴的垂线,交直线EF于N;设出K点的横坐标,根据抛物线和直线EF的解析式,即可表示出K、N的纵坐标,也就能得到KN的长,以KN为底,F、E横坐标差的绝对值为高,可求出△KEF的面积,由此可得到关于△KEF的面积与K点横坐标的函数关系式,根据所得函数的性质即可求出其面积的最大值及对应的K点坐标
解答 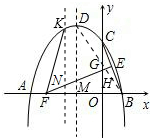 解:(1)由题意,得 $\left\{\begin{array}{l}16a-4b+4=0\\ 4a+2b+4=0\end{array}\right.$,
解:(1)由题意,得 $\left\{\begin{array}{l}16a-4b+4=0\\ 4a+2b+4=0\end{array}\right.$,
解得$a=-\frac{1}{2}$,b=-1,
所以抛物线的解析式为$y=-\frac{1}{2}{x^2}-x+4$,顶点D的坐标为(-1,$\frac{9}{2}$);
(2)设抛物线的对称轴与x轴交于点M.
∵EF垂直平分BC,
∴C关于直线EG的对称点为B,连结BD交于EF于一点,
∴这一点为所求点H,使DH+CH最小,即最小为DH+CH=DH+HB=BD=$\sqrt{B{M^2}+D{M^2}}=\frac{3}{2}\sqrt{13}$.
而 $CD=\sqrt{{1^2}+{{(\frac{9}{2}-4)}^2}}=\frac{{\sqrt{5}}}{2}$.
∴△CDH的周长最小值为CD+DH+CH=$\frac{{\sqrt{5}+3\sqrt{13}}}{2}$,
设直线BD的解析式为y=k1x+b,则 $\left\{\begin{array}{l}2{k_1}+{b_1}=0\\-{k_1}+{b_1}=\frac{9}{2}\end{array}\right.$,
解得 ${k_1}=-\frac{3}{2}$,b1=3.
所以直线BD的解析式为y=$-\frac{3}{2}$x+3,
由于BC=2$\sqrt{5}$,CE=$\frac{1}{2}$BC=$\sqrt{5}$,Rt△CEG∽△COB,
得 CE:CO=CG:CB,所以 CG=2.5,GO=1.5.G(0,1.5).
同理可求得直线EF的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$,
联立直线BD与EF的方程,解得使△CDH的周长最小的点H($\frac{3}{4}$,$\frac{15}{8}$);
(3)设K(t,$-\frac{1}{2}{t^2}-t+4$),xF<t<xE.
过K作x轴的垂线交EF于N.
则KN=yK-yN=$-\frac{1}{2}{t^2}-t+4$-($\frac{1}{2}$t+$\frac{3}{2}$)=$-\frac{1}{2}{t^2}-\frac{3}{2}t+\frac{5}{2}$.
所以 S△EFK=S△KFN+S△KNE=$\frac{1}{2}$KN(t+3)+$\frac{1}{2}$KN(1-t)=2KN=-t2-3t+5=-(t+$\frac{3}{2}$)2+$\frac{29}{4}$.
即当t=-$\frac{3}{2}$时,△EFK的面积最大,最大面积为$\frac{29}{4}$,此时K(-$\frac{3}{2}$,$\frac{35}{8}$).
点评 本题是二次函数的综合类试题,考查了二次函数解析式的确定、轴对称的性质、相似三角形的判定和性质、三角形面积的求法、二次函数的应用等知识,难度较大.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
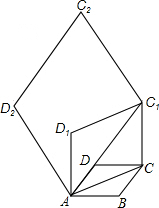 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )| A. | 9 | B. | 9$\sqrt{3}$ | C. | 27 | D. | 27$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | |
| B. | 两点之间,线段最短 | |
| C. | 经过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 如果两条直线都和第三条直线平行,那么这两条直线也相互平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com