
���� �ٸ��ݷǸ����ĺ�Ϊ0�����Ϊ0����Ӧ���ǵ�A��B��P����֮���λ�ù�ϵ�Ķ��ֿ��ܽ��⣻�ۢ������е�����ת���߶�֮��ı��ֹ�ϵ�ó���
��� �⣺�١�|a+2|+��b-1��2=0��
��a+2=0��b-1=0����a=-2��b=1��
��|AB|=|a-b|=3��
��ٲ���ȷ��
��2����P�ڵ�A���ʱ��
|PA|-|PB|=-��|PB|-|PA|��=-|AB|=-3��2��
��P�ڵ�B�Ҳ�ʱ��
|PA|-|PB|=|AB|=3��2��
��������������ĵ�P�����ڣ�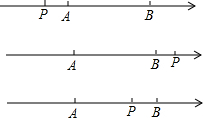
��P��A��B֮��ʱ��|PA|=|x-��-2��|=x+2��|PB|=|x-1|=1-x��
��|PA|-|PB|=2����x+2-��1-x��=2��
��x=$\frac{1}{2}$����x��ֵΪ$\frac{1}{2}$��
���P����
�����ȷ��
�����P�������϶�Ӧ����Ϊx��
��|PM|+|PN|=$\frac{1}{2}$|PB|+$\frac{1}{2}$|PA|=$\frac{1}{2}$��|PB|+|PA|��=$\frac{1}{2}$��1-x-x-2��=-$\frac{2x+1}{2}$��
��۲���ȷ��
��|PN|-|PM|��ֵ���䣬ֵΪ$\frac{5}{2}$��
��|PN|-|PM|=$\frac{1}{2}$|PB|-$\frac{1}{2}$|PA|=$\frac{1}{2}$��|PB|-|PA|��=$\frac{1}{2}$|AB|=$\frac{5}{2}$��
��|PN|-|PM|=$\frac{5}{2}$��
�����ȷ��
�ʴ�Ϊ���ڢܣ�
���� �������˷������۵�˼�룬������˼ά�������ԣ��ڽ�������Ƶ�����ʱ��Ҫ��ֹ©�⣮�����е�����ת���߶�֮��ı��ֹ�ϵ�ǽ���Ĺؼ����ڲ�ͬ����������ѡ�����IJ�ͬ��ʾ�����������ڽ���ļ���ԣ�ͬʱ����������߶εĺ͡��������ת���߶�֮���������ϵҲ��ʮ�ֹؼ���һ�㣮


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$cm | B�� | 4$\sqrt{2}$cm | C�� | 8$\sqrt{2}$cm | D�� | ���Ͻ��۶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
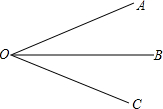 ��ͼ��AOC=60�㣬OB�ǡ�AOC��ƽ���ߣ����ٰѡ�AOB�ĵȷ֣�ÿһ���Ƕ��ٶȽǣ���ȷ���֣���
��ͼ��AOC=60�㣬OB�ǡ�AOC��ƽ���ߣ����ٰѡ�AOB�ĵȷ֣�ÿһ���Ƕ��ٶȽǣ���ȷ���֣����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a+b}{{a}^{2}b}$=$\frac{ac+bc}{{a}^{2}bc}$ | B�� | $\frac{2x}{{x}^{2}{+y}^{2}}$=$\frac{2x+1}{{x}^{2}{+y}^{2}+1}$ | ||
| C�� | $\frac{2x}{{x}^{2}y+xy}$=$\frac{2}{xy+y}$ | D�� | $\frac{{x}^{2}{+y}^{2}}{x+y}$=xy |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
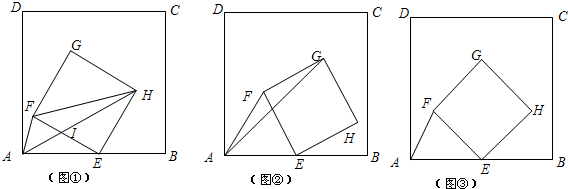
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com