
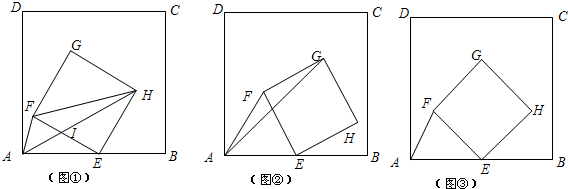
分析 (1)①易证A、F、H在以点E为圆心,AE为半径的圆上,根据圆周角定理可得∠FAH=$\frac{1}{2}$∠FEH=45°;
②由于FH=$\sqrt{2}$EF=$\sqrt{2}$AE,要证2AE2=AH•IH,只需证到FH2=AH•IH,只需证到△FHI∽△AHF即可;
(2)连接DE与直线AG交于点N,连接NB,如图②,易证△AFG≌△AEH,则有∠FAG=∠EAH,从而可得∠DAG=∠GAE.由AD=AB可得点D与点B关于直线AG对称,从有而ND=NB,从而可求得EN+BN+EB=2$\sqrt{5}$+2.根据两点之间线段最短可得:当点J运动到点N处,△EBJ的周长最短,问题得以解决;
(3)点E运动的过程中,依次出现图③a、图③b、图③c、图③d、图③e、图③f的情况,只需运用割补法分别求出图③a、图③c、图③e中S与t的关系式,运用方程思想求出图③b、图③d、图③f中对应t的值,就可解决问题.
解答 解:(1)①证明:∵EA=EF=EH,
∴A、F、H在以点E为圆心,AE为半径的圆上,如图①,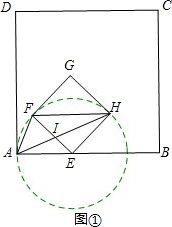
∴∠FAH=$\frac{1}{2}$∠FEH=45°,
∴∠FAH的度数是一个常数;
②∵四边形EFGH是正方形,
∴∠EFH=45°,∠FEH=90°,FH=$\sqrt{2}$EF=$\sqrt{2}$AE,
∵∠FHI=∠AHF,∠HFI=∠HAF=45°,
∴△FHI∽△AHF,
∴$\frac{IH}{FH}$=$\frac{FH}{AH}$,
∴FH2=AH•IH,
∴2AE2=AH•IH;
(2)连接DE与直线AG交于点N,连接NB,如图②.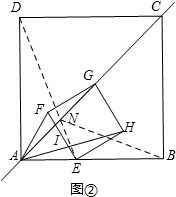
∵∠AEF=60°,EA=EF,
∴△AEF是等边三角形,
∴∠AFE=∠AEF=60°,AF=AE.
∵四边形EFGH是正方形,
∴∠EFG=∠FEH=90°,FG=EH,
∴∠AFG=∠AEH=150°.
在△AFG和△AEH中,
$\left\{\begin{array}{l}{AF=AE}\\{∠AFG=∠AEH}\\{FG=EH}\end{array}\right.$,
∴△AFG≌△AEH(SAS),
∴∠FAG=∠EAH,
∴∠FAH=∠GAE=45°,
∴∠DAG=90°-∠GAE=45°=∠GAE.
∵AD=AB,∴点D与点B关于直线AG对称,
∴ND=NB,
∴EN+BN=EN+DN=DE.
∵点E是AB的中点,
∴AE=BE=2.
在Rt△DAE中,
DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴EN+BN+EB=2$\sqrt{5}$+2.
根据两点之间线段最短可得:
当点J运动到点N处,△EBJ的周长最短,此时周长为2$\sqrt{5}$+2;
(3)①如图③a,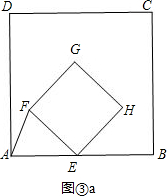
EF=EA=1×t=t,则有S=t2;
②如图③b,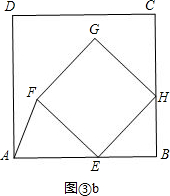
此时点H在线段BC上,
在Rt△EBH中,
∠B=90°,∠HEB=180°-90°-45°=45°,
∴EH=$\sqrt{2}$EB,
∴t=$\sqrt{2}$(4-t),
解得:t=8-4$\sqrt{2}$;
③如图③c,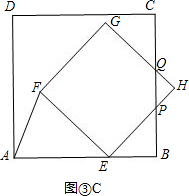
则有EP=$\sqrt{2}$EB=$\sqrt{2}$(4-t),EH=EF=t,∠EPB=45°,
∴∠QPH=∠EPB=45°,PH=t-[$\sqrt{2}$(4-t)]=($\sqrt{2}$+1)t-4$\sqrt{2}$,
∴QH=PH=($\sqrt{2}$+1)t-4$\sqrt{2}$,
∴S=t2-$\frac{1}{2}$[($\sqrt{2}$+1)t-4$\sqrt{2}$]2=-($\sqrt{2}$+$\frac{1}{2}$)t2+(8+4$\sqrt{2}$)t-16;
④如图③d,点G在线段DC上,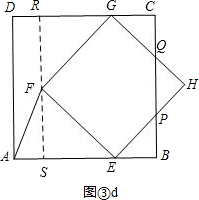
过点F作FS⊥AB,交AB于点S,交DC于点R,
则有SR⊥DC,∠SFE=45°,∠RFG=45°,
∴RF=$\frac{\sqrt{2}}{2}$FG=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$t,FS=$\frac{\sqrt{2}}{2}$t,
∴RS=$\sqrt{2}$t=4,
∴t=2$\sqrt{2}$;
如图③e,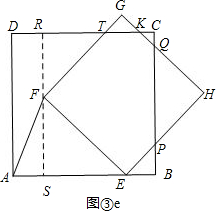
则有FS=$\frac{\sqrt{2}}{2}$t,RF=4-$\frac{\sqrt{2}}{2}$t,FT=$\sqrt{2}$RF=4$\sqrt{2}$-t,
GK=GT=GF-FT=EF-FT=t-(4$\sqrt{2}$-t)=2t-4$\sqrt{2}$,
QH=PH=EH-EP=($\sqrt{2}$+1)t-4$\sqrt{2}$,
∴S=t2-$\frac{1}{2}$[($\sqrt{2}$+1)t-4$\sqrt{2}$]2-$\frac{1}{2}$[2t-4$\sqrt{2}$]2=-($\sqrt{2}$+$\frac{5}{2}$)t2+(8+12$\sqrt{2}$)t-32;
如图③f,点C在线段GH上,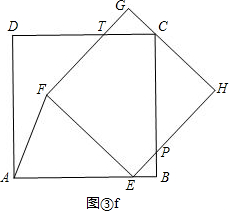
则有BE=BP=4-t,PC=4-(4-t)=t,
PH=EH-EP=EF-$\sqrt{2}$EB=t-$\sqrt{2}$(4-t)=($\sqrt{2}$+1)t-4$\sqrt{2}$.
∵PC=$\sqrt{2}$PH,
∴t=$\sqrt{2}$[($\sqrt{2}$+1)t-4$\sqrt{2}$],
解得:t=8$\sqrt{2}$-8.
综上所述:当0<t≤8-4$\sqrt{2}$时,S=t2;
当8-4$\sqrt{2}$<t≤2$\sqrt{2}$时,S=-($\sqrt{2}$+$\frac{1}{2}$)t2+(8+4$\sqrt{2}$)t-16;
当2$\sqrt{2}$<t≤8$\sqrt{2}$-8时,S=-($\sqrt{2}$+$\frac{5}{2}$)t2+(8+12$\sqrt{2}$)t-32.
点评 本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、圆周角定理、勾股定理、正方形的性质、旋转的性质、轴对称性、两点之间线段最短等知识,有一定的难度,运用分类讨论的思想是解决第(3)小题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
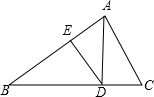 如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )
如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 5 | C. | 7 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大10倍 | B. | 缩小10倍 | C. | 是原来的$\frac{2}{3}$ | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com