
【题目】如图,AB∥DE,AB=DE,BF=EC.
(1)求证:AC∥DF;
(2)若CF=1个单位长度,能由△ABC经过图形变换得到△DEF吗?若能,请你用轴对称、平移或旋转等描述你的图形变换过程;若不能,说明理由.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.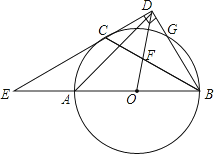
(1)求证:CD是⊙O的切线.
(2)若![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在2的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
(1)则点A,B,C的坐标分别是A( , ),B( , ),C( , );
(2)设经过A,B两点的抛物线解析式为y=![]() (x﹣5)2+k,它的顶点为E,求证:直线EA与⊙M相切;
(x﹣5)2+k,它的顶点为E,求证:直线EA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1 , P2 , P3 , …,Pn﹣1 , 过每个分点作x轴的垂线分别交直线AB于点T1 , T2 , T3 , …,Tn﹣1 , 用S1 , S2 , S3 , …,Sn﹣1分别表示Rt△T1OP1 , Rt△T2P1P2 , …,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则当n=2015时,S1+S2+S3+…+Sn﹣1= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2 , 再依次连接△A2B2C2的三边中点得△A3B3C3 , …,则△A5B5C5的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=![]() ,且
,且![]() =
=![]() ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=![]() x2+
x2+![]() x+c经过点E,且与AB边相交于点F.
x+c经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.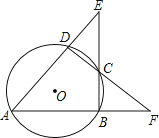
(1)若∠E=∠F时,求证:∠ADC=∠ABC;
(2)(2)若∠E=∠F=42°时,求∠A的度数
(3)(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣4,![]() ),B(﹣1,2)是一次函数y1=ax+b与反比例函数y2=
),B(﹣1,2)是一次函数y1=ax+b与反比例函数y2=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)根据图象直接回答:在第二象限内,当x取何值时,y1﹣y2>0?
(2)求一次函数解析式及m的值;
(3)P是线段AB上一点,连接PC,PD,若△PCA和△PDB面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com