
 如图,已知△ABC的面积是1,D、E、F和G、H、I分别是BC和AC边上的4等分点,则图中阴影部分的面积是( )
如图,已知△ABC的面积是1,D、E、F和G、H、I分别是BC和AC边上的4等分点,则图中阴影部分的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
| CI |
| CA |
| CF |
| CB |
| 1 |
| 4 |
| 1 |
| 16 |
| IF |
| AB |
| CI |
| CA |
| 1 |
| 4 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
| 4 |
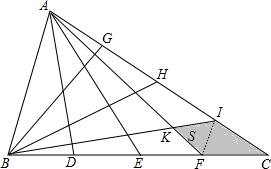 设S△IFK的面积为S,
设S△IFK的面积为S,| CI |
| CA |
| CF |
| CB |
| 1 |
| 4 |
| S△CIF |
| S△ABC |
| CI |
| CA |
| 1 |
| 16 |
| IF |
| AB |
| CI |
| CA |
| 1 |
| 4 |
| S△IFK |
| S△ABK |
| 1 |
| 16 |
| 1 |
| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |
| 80 |
| 3 |
| 80 |
| 1 |
| 16 |
| 1 |
| 10 |


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
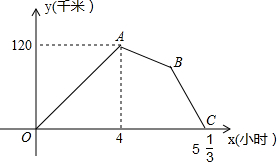 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:| 5 |
| 6 |
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
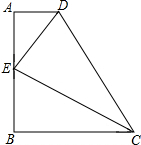 如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:
如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com