
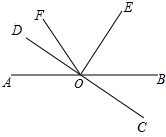
 如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.
如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.分析 (1)根据∠AOD=20°和∠DOF:∠FOB=1:7,求出∠BOF等于140°,所以∠EOB等于70°;
(2)利用(1)中所求,进而得出∠EOC等于90°得出答案即可.
解答 解:(1)∵OE平分∠BOF,
∴∠BOE=EOF,
∵∠DOF:∠FOB=1:7,∠AOD=20°,
∴∠DOF=$\frac{1}{8}$∠BOD=$\frac{1}{8}$×(180°-20°)=20°,
∴∠BOF=140°,
∴∠BOE=$\frac{1}{2}$∠BOE=$\frac{1}{2}$∠BOF=$\frac{1}{2}$×140°=70°;
(2)由(1)得:∠EOC=∠BOC+∠EOB=70°+20°=90°,
则射线OE与直线CD垂直.
点评 此题主要考查了对顶角、邻补角以及角平分线的性质,主要利用对顶角相等,邻补角的定义和角平分线的定义求解.


科目:初中数学 来源: 题型:解答题
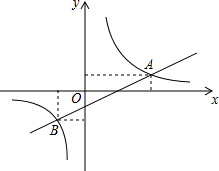 如图,反比例函数y=$\frac{k}{x}$(k≠0)和一次函数y=ax+b(a≠0)的图象交于A(4,$\frac{3}{2}$),B(-2,n) 两点.
如图,反比例函数y=$\frac{k}{x}$(k≠0)和一次函数y=ax+b(a≠0)的图象交于A(4,$\frac{3}{2}$),B(-2,n) 两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
候选人 | 面试 | 笔试 | ||
| 形体 | 口才 | 专业水平 | 创新能力 | |
| 甲 | 86 | 90 | 96 | 92 |
| 乙 | 92 | 88 | 95 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com