
候选人 | 面试 | 笔试 | ||
| 形体 | 口才 | 专业水平 | 创新能力 | |
| 甲 | 86 | 90 | 96 | 92 |
| 乙 | 92 | 88 | 95 | 93 |
分析 (1)由形体、口才、专业水平、创新能力按照4:6:5:5的比确定,根据加权平均数的计算方法分别计算不同权的平均数,比较即可,
(2)由面试成绩中形体占15%,口才占20%,笔试成绩中专业水平占40%,创新能力占25%,根据加权平均数的计算方法分别计算不同权的平均数,比较即可,
解答 解:(1)形体、口才、专业水平、创新能力按照4:6:5:5的比确定,
则甲的平均成绩为$\frac{86×4+90×6+96×5+92×5}{4+6+5+5}$=91.2.
乙的平均成绩为$\frac{92×4+88×6+95×5+93×5}{4+6+5+5}$=91.8.
乙的成绩比甲的高,所以应该录取乙.
(2)面试成绩中形体占15%,口才占20%,笔试成绩中专业水平占40%,创新能力占25%,
则甲的平均成绩为86×15%+90×20%+96×40%+92×25%=92.3.
乙的平均成绩为92×15%+88×20%+95×40%+93×25%=92.65.
甲的成绩比乙的低,所以应该录取乙.
点评 本题考查的是加权平均数的求法.本题易出现的错误是求形体、口才、专业水平、创新能力成绩的平均数,对平均数的理解不正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
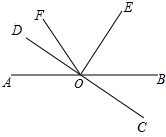 如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.
如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
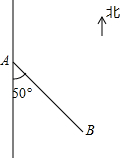 如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,用( )可以确定2班相对于1班的位置.
如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,用( )可以确定2班相对于1班的位置.| A. | 北偏东50°,5km | B. | 北偏西50°,5km | C. | 南偏东50°,5km | D. | 南偏西50°,5km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com