
【题目】如图,在△ABC 中,AB=AC,∠BAC=120°,AC 的垂直平分线交 BC 于 F,交 AC 于 E,交 BA 的延长线于 G,若 EG=3,则 BF 的长是______.
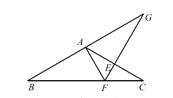
【答案】4
【解析】
根据线段垂直平分线得出AE=EC,∠AEG=∠AEF=90°,求出∠B=∠C=∠G=30°,根据勾股定理和含30°角的直角三角形性质求出AE和EF,即可求出FG,再求出BF=FG即可
∵AC的垂直平分线FG,
∴AE=EC,∠AEG=∠AEF=90°,
∵∠BAC=120°,
∴∠G=∠BAC-∠AEG=120°-90°=30°,
∵∠BAC=120°,AB=AC,
∴∠B=∠C=![]() (180°-∠BAC)=30°,
(180°-∠BAC)=30°,
∴∠B=∠G,
∴BF=FG,
∵在Rt△AEG中,∠G=30°,EG=3,
∴AG=2AE,
即(2AE)2=AE2+32,
∴AE=![]() (负值舍去)
(负值舍去)
即CE=![]() ,
,
同理在Rt△CEF中,∠C=30°,CF=2EF,
(2EF)2=EF2+(![]() )2,
)2,
∴EF=1(负值舍去),
∴BF=GF=EF+CE=1+3=4,
故答案为:4.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图及探究:
已知:线段AB=a.
(1)完成尺规作图:

点P在线段AB所在直线上方,PA=PB,且点P到AB的距离等于![]() ,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
(2)若将(1)中的条件“点P到AB的距离等于![]() ”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为
”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为![]() ,点Q的位置记为
,点Q的位置记为![]() ,连接
,连接![]() ,并直接回答∠
,并直接回答∠![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P,过 P 作 MN∥AB 交 AC 于M,交 BC 于 N,且 AM=8,BN=5,则 MN=( )
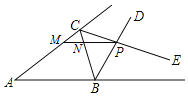
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用关于坐标系轴对称的点的坐标的特点.
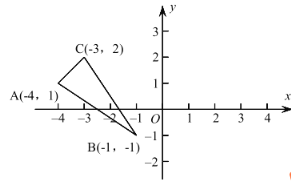
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出各点坐标:△A1( ),B1( ),C1 ( ).
(3)直接写出△ABC 的面积______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,175,170,则下列说法错误的是( )
A. 这组数据的平均数是169 B. 这组数据的众数是170
C. 这组数据的中位数是169 D. 这组数据的方差是66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
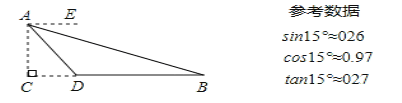
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com