
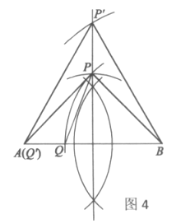
”¾ĢāÄæ”æ³ß¹ę×÷Ķ¼¼°Ģ½¾æ£ŗ
ŅŃÖŖ£ŗĻ߶ĪAB=a£®
£Ø1£©Ķź³É³ß¹ę×÷Ķ¼£ŗ

µćPŌŚĻ߶ĪABĖłŌŚÖ±ĻßÉĻ·½£¬PA=PB£¬ĒŅµćPµ½ABµÄ¾ąĄėµČÓŚ![]() £¬Į¬½ÓPA£¬PB£¬ŌŚĻ߶ĪABÉĻÕŅµ½Ņ»µćQŹ¹µĆQB=PB£¬Į¬½ÓPQ£¬²¢Ö±½Ó»Ų“š”ĻPQBµÄ¶ČŹż£»
£¬Į¬½ÓPA£¬PB£¬ŌŚĻ߶ĪABÉĻÕŅµ½Ņ»µćQŹ¹µĆQB=PB£¬Į¬½ÓPQ£¬²¢Ö±½Ó»Ų“š”ĻPQBµÄ¶ČŹż£»
£Ø2£©Čō½«£Ø1£©ÖŠµÄĢõ¼ž”°µćPµ½ABµÄ¾ąĄėµČÓŚ![]() ”±Ģę»»ĪŖ”°PBČ”µĆ×ī“óÖµ”±£¬ĘäÓąĖłÓŠĢõ¼ž¶¼²»±ä£¬“ĖŹ±µćPµÄĪ»ÖĆ¼ĒĪŖ
”±Ģę»»ĪŖ”°PBČ”µĆ×ī“óÖµ”±£¬ĘäÓąĖłÓŠĢõ¼ž¶¼²»±ä£¬“ĖŹ±µćPµÄĪ»ÖĆ¼ĒĪŖ![]() £¬µćQµÄĪ»ÖĆ¼ĒĪŖ
£¬µćQµÄĪ»ÖĆ¼ĒĪŖ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬²¢Ö±½Ó»Ų“š”Ļ
£¬²¢Ö±½Ó»Ų“š”Ļ![]() µÄ¶ČŹż£®
µÄ¶ČŹż£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£¬67.5![]() £»£Ø2£©60
£»£Ø2£©60![]()
”¾½āĪö”æ
£Ø1£©×÷Ļ߶ĪABµÄ“¹Ö±Ę½·ÖĻßDE£¬DĪŖ“¹×ć£¬ŌŚÉäĻßDEÉĻ½ŲČ”DP=![]() £¬Į¬½ÓPA£¬PB¼“æɽā¾öĪŹĢā£®
£¬Į¬½ÓPA£¬PB¼“æɽā¾öĪŹĢā£®
£Ø2£©×÷µČ±ßČż½ĒŠĪP”äAB¼“æɽā¾öĪŹĢā£®
½ā£ŗ£Ø1£©×÷Ķ¼¼ūĶ¼4£®ČēĶ¼£¬µćP¼“ĪŖĖłĒó£®
ŅņĪŖ£ŗµćPµ½ABµÄ¾ąĄėµČÓŚ![]() £¬PA=PB
£¬PA=PB
ĖłŅŌ£ŗ![]() ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻPBA=45”ć
ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻPBA=45”ć
”ßBP=BQ£¬£¬ ”ą”ĻPQB=”ĻBPQ=67.5”ć£®
£Ø2£©×÷Ķ¼¼ūĶ¼4£¬ µ±P”äBČ”µĆ×ī“óÖµŹ±£¬”÷ABP”äŹĒµČ±ßČż½ĒŠĪ£¬
ĖłŅŌ![]() ŹĒµČ±ßČż½ĒŠĪ£¬ ”ą
ŹĒµČ±ßČż½ĒŠĪ£¬ ”ą![]() =60”ć£®
=60”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬A”¢P”¢B”¢CŹĒ”ŃOÉĻµÄĖÄµć£¬”ĻAPC=”ĻCPB=60”ć£¬¹żµćC×÷CM”ĪBP½»PAµÄŃÓ³¤ĻßÓŚµćM£®
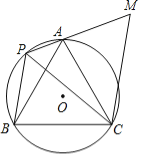
£Ø1£©ĒóÖ¤£ŗ”÷ACM”Õ”÷BCP£»
£Ø2£©ČōPA=1£¬PB=2£¬Ēó”÷PCMµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¶Ū½ĒČż½ĒŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬¶Æµć
£¬¶Æµć![]() “Ó
“Ó![]() µć³ö·¢µ½
µć³ö·¢µ½![]() µćÖ¹£¬¶Æµć
µćÖ¹£¬¶Æµć![]() “Ó
“Ó![]() µć³ö·¢µ½
µć³ö·¢µ½![]() µćÖ¹£¬µć
µćÖ¹£¬µć![]() ŌĖ¶ÆµÄĖŁ¶ČĪŖ
ŌĖ¶ÆµÄĖŁ¶ČĪŖ![]() £¬µć
£¬µć![]() ŌĖ¶ÆµÄĖŁ¶ČĪŖ
ŌĖ¶ÆµÄĖŁ¶ČĪŖ![]() £¬Čē¹ūĮ½µćĶ¬Ź±æŖŹ¼ŌĖ¶Æ£¬ÄĒĆ“,
£¬Čē¹ūĮ½µćĶ¬Ź±æŖŹ¼ŌĖ¶Æ£¬ÄĒĆ“,
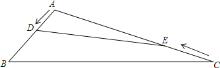
![]() ČōAD=AE£¬Ēó
ČōAD=AE£¬Ēó![]() Öµ£®
Öµ£®
![]() Čō”÷ADEŗĶ”÷ABCĻąĖĘ£¬Ēó
Čō”÷ADEŗĶ”÷ABCĻąĖĘ£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
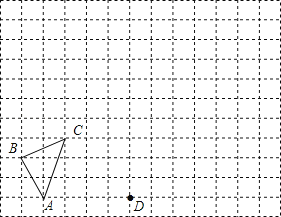
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÓɱ߳¤ĪŖ1µÄµ„Ī»Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬°“ŅŖĒó»³ö×ų±źĻµ¼°”÷A1B1C1¼°”÷A2B2C2£»
£Ø1£©ČōµćA”¢CµÄ×ų±ź·Ö±šĪŖ£Ø©3£¬0£©”¢£Ø©2£¬3£©£¬Ēė»³öĘ½ĆęÖ±½Ē×ų±źĻµ²¢Öø³öµćBµÄ×ų±ź£»
£Ø2£©»³ö”÷ABC¹ŲÓŚyÖį¶Ō³ĘŌŁĻņÉĻĘ½ŅĘ1øöµ„Ī»ŗóµÄĶ¼ŠĪ”÷A1B1C1£»
£Ø3£©ŅŌĶ¼ÖŠµÄµćDĪŖĪ»ĖĘÖŠŠÄ£¬½«”÷A1B1C1×÷Ī»Ėʱ任ĒŅ°Ń±ß³¤·Å“óµ½ŌĄ“µÄĮ½±¶£¬µĆµ½”÷A2B2C2£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬SĶ¬Ń§°ŃŅ»ÕÅ6”Į6µÄÕż·½ŠĪĶųøńÖ½ĻņÉĻŌŁĻņÓŅ¶ŌÕŪĮ½“Īŗó°“Ķ¼»ŹµĻߣ¬¼ōČ„¶ąÓą²æ·ÖÖ»ĮōĻĀŅõÓ°²æ·Ö£¬Č»ŗóÕ¹æŖĢÆĘ½ŌŚŅ»øöĘ½ĆęÄŚµĆµ½ĮĖŅ»·ł¼ōÖ½Ķ¼°ø£®TĶ¬Ń§Ėµ£ŗ”°ĪŅ²»ÓĆ¼ōÖ½£¬ĪŅÖ±½ÓŌŚÄćµÄĶ¼1¢Ś»ł“”ÉĻ£¬Ķعż”®ÄęĻņ»¹Ō”Ƶķ½Ź½ŅĄ“Ī»³öĻąÓ¦µÄÓėŌĶ¼ŠĪ³ÉÖį¶Ō³ĘµÄĶ¼ŠĪŅ²ÄÜµĆ³ö×īŗóµÄĶ¼°ø£®”±»Ķ¼¹ż³ĢČēĶ¼2ĖłŹ¾£®
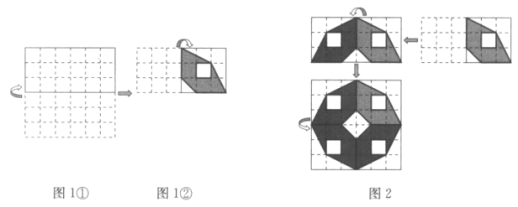
¶ŌÓŚĶ¼3ÖŠµÄĮķŅ»ÖÖ¼ōÖ½·½Ź½£¬Ēė·ĀÕÕĶ¼2ÖŠ”°ÄęĻņ»¹Ō”±µÄ·½Ź½£¬ŌŚĶ¼4¢ŁÖŠµÄÕż·½ŠĪĶųøńÖŠ»³ö»¹ŌŗóµÄĶ¼°ø£¬²¢ÅŠ¶ĻĖüÓėĶ¼2ÖŠ×īŗóµĆµ½µÄĶ¼°øŹĒ·ńĻąĶ¬£®
“š£ŗ”õĻąĶ¬£»”õ²»ĻąĶ¬£®£ØŌŚĻąÓ¦µÄ·½æņÄŚ“ņ¹“£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1ÖŠµÄČżÖÖĒéæöĖłŹ¾£¬¶ŌÓŚĘ½ĆęÄŚµÄµćM£¬µćN£¬µćP£¬Čē¹ū½«Ļ߶ĪPMČʵćPĖ³Ź±ÕėŠż×Ŗ90”ćÄܵƵ½Ļ߶ĪPN£¬¾Ķ³ĘµćNŹĒµćM¹ŲÓŚµćPµÄ”°Õż¾Ųµć”±£®
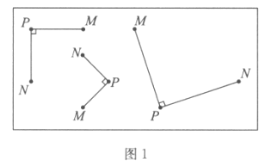
£Ø1£©ŌŚČēĶ¼2ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ŅŃÖŖ
ÖŠ£¬ŅŃÖŖ![]() £¬
£¬![]() £®
£®
¢ŁŌŚµćP£¬µćQÖŠ£¬___________ŹĒµćS¹ŲÓŚŌµćOµÄ”°Õż¾Ųµć”±£»
¢ŚŌŚS£¬P£¬Q£¬MÕāĖĵćÖŠŃ”ŌńŗĻŹŹµÄČżµć£¬Ź¹µĆÕāČżµćĀś×ć£ŗ
µć_________ŹĒµć___________¹ŲÓŚµć___________µÄ”°Õż¾Ųµć”±£¬Š“³öŅ»ÖÖĒéæö¼“æÉ£»
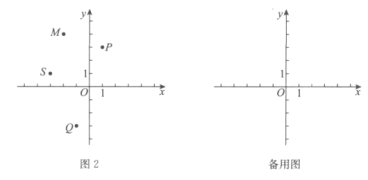
£Ø2£©ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬Ö±Ļß
ÖŠ£¬Ö±Ļß![]() ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬µćA¹ŲÓŚµćBµÄ”°Õż¾Ųµć”±¼ĒĪŖµćC£¬×ų±źĪŖ
ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬µćA¹ŲÓŚµćBµÄ”°Õż¾Ųµć”±¼ĒĪŖµćC£¬×ų±źĪŖ![]() £®
£®
¢Łµ±µćAŌŚxÖįµÄÕż°ėÖįÉĻĒŅOAŠ”ÓŚ3Ź±£¬ĒóµćCµÄŗį×ų±ź![]() µÄÖµ£»
掙术
¢ŚČōµćCµÄׯ×ų±ź![]() Āś×ć
Āś×ć![]() £¬Ö±½ÓŠ“³öĻąÓ¦µÄkµÄȔֵ·¶Ī§£®
£¬Ö±½ÓŠ“³öĻąÓ¦µÄkµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABC ÖŠ£¬AB£½AC£¬”ĻBAC£½120”ć£¬AC µÄ“¹Ö±Ę½·ÖĻß½» BC ÓŚ F£¬½» AC ÓŚ E£¬½» BA µÄŃÓ³¤ĻßÓŚ G£¬Čō EG£½3£¬Ōņ BF µÄ³¤ŹĒ______£®
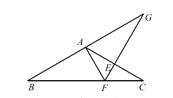
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§æĪĶāŠĖȤ»ī¶ÆŠ”×é×¼±øĪ§½ØŅ»øö¾ŲŠĪĆēĘŌŌ°£¬ĘäÖŠŅ»±ßææĒ½£¬ĮķĶāČż±ßÓɳ¤ĪŖ30Ć׵ĥ鰏Ī§³É£®ŅŃÖŖĒ½³¤ĪŖ18Ć×£ØČēĶ¼ĖłŹ¾£©£¬ÉčÕāøöĆēĘŌŌ°“¹Ö±ÓŚĒ½µÄŅ»±ß³¤ĪŖxĆ×£®
£Ø1£©ČōĆēĘŌŌ°µÄĆ껿ĪŖ72Ę½·½Ć×£¬Ēóx£»
£Ø2£©ČōĘ½ŠŠÓŚĒ½µÄŅ»±ß³¤²»Š”ÓŚ8Ć×£¬ÕāøöĆēĘŌŌ°µÄĆ껿ӊ×ī“óÖµŗĶ×īŠ”ÖµĀš£æČē¹ūÓŠ£¬Ēó³ö×ī“óÖµŗĶ×īŠ”Öµ£»Čē¹ūƻӊ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ»ĘŃŅijŠ£°įĒØŗ󣬊čŅŖŌö¼Ó½ĢŹ¦ŗĶѧɜµÄĒŽŹŅŹżĮ棬ĒŽŹŅÓŠČżĄą£¬·Ö±šĪŖµ„ČĖ¼ä£Ø¹©Ņ»øöČĖ×”ĖŽ£©£¬Ė«ČĖ¼ä£Ø¹©Į½øöČĖ×”ĖŽ£©£¬ĖÄČĖ¼ä£Ø¹©ĖÄøöČĖ×”ĖŽ£©£®ŅņŹµ¼ŹŠčŅŖ£¬µ„ČĖ¼äµÄŹżĮæŌŚ20ÖĮ30Ö®¼ä£Ø°üĄØ20ŗĶ30£©£¬ĒŅĖÄČĖ¼äµÄŹżĮæŹĒĖ«ČĖ¼äµÄ5±¶£®
£Ø1£©Čō2018ğѧŠ£ĒŽŹŅŹżĪŖ64øö£¬ŅŌŗó֚ğŌö¼Ó£¬Ō¤¼Ę2020ÄźĒŽŹŅŹż“ļµ½121øö£¬Ēó2018ÖĮ2020ÄźĒŽŹŅŹżĮæµÄÄźĘ½¾łŌö³¤ĀŹ£»
£Ø2£©ČōČżĄą²»Ķ¬µÄĒŽŹŅµÄ×ÜŹżĪŖ121øö£¬Ōņ×ī¶ąæɹ©¶ąÉŁŹ¦Éś×”ĖŽ£æ
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com