
【题目】在钝角三角形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发到
点出发到![]() 点止,动点
点止,动点![]() 从
从![]() 点出发到
点出发到![]() 点止,点
点止,点![]() 运动的速度为
运动的速度为![]() ,点
,点![]() 运动的速度为
运动的速度为![]() ,如果两点同时开始运动,那么,
,如果两点同时开始运动,那么,
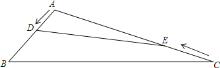
![]() 若AD=AE,求
若AD=AE,求![]() 值.
值.
![]() 若△ADE和△ABC相似,求
若△ADE和△ABC相似,求![]() 的值.
的值.
【答案】(1)t=4;(2)t=3或4.8
【解析】
(1)先有![]() ,
,![]() ,及点D、E速度、时间表示出AD、AE的长即可解答.
,及点D、E速度、时间表示出AD、AE的长即可解答.
(2)如果以点A、D、E为顶点的三角形与△ABC相似,由于A与A对应,那么分两种情况:①D与B对应;②D与C对应.再根据相似三角形的性质分别作答.
(1)∵,![]() ,
,![]() ,设运动t秒时,则AD=t,CE=2t,AE=AC-CE=12-2t
,设运动t秒时,则AD=t,CE=2t,AE=AC-CE=12-2t
当AD=AE时,有t=12-2t,解得:t=4.
故正确答案为:4秒
(2)解:如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,则AD=t,CE=2t,AE=AC-CE=12-2t.
①当D与B对应时,有△ADE∽△ABC.
∴AD:AB=AE:AC,
∴t:6=(12-2t):12,
∴t=3;
②当D与C对应时,有△ADE∽△ACB.
∴AD:AC=AE:AB,
∴t:12=(12-2t):6,
∴t=4.8.
所以当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒.
故正确答案为:3秒或4.8秒.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是( )
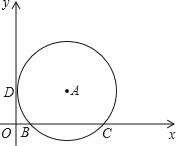
A. (5,4) B. (4,5) C. (5,3) D. (3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
⑴先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为_______,若A为随机事件,则m的取值为______;
⑵若从袋中随机摸出2个球,正好红球、黑球各1个,用列表法与树状图法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求EF:BF的值.
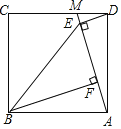
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图及探究:
已知:线段AB=a.
(1)完成尺规作图:

点P在线段AB所在直线上方,PA=PB,且点P到AB的距离等于![]() ,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
,连接PA,PB,在线段AB上找到一点Q使得QB=PB,连接PQ,并直接回答∠PQB的度数;
(2)若将(1)中的条件“点P到AB的距离等于![]() ”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为
”替换为“PB取得最大值”,其余所有条件都不变,此时点P的位置记为![]() ,点Q的位置记为
,点Q的位置记为![]() ,连接
,连接![]() ,并直接回答∠
,并直接回答∠![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,175,170,则下列说法错误的是( )
A. 这组数据的平均数是169 B. 这组数据的众数是170
C. 这组数据的中位数是169 D. 这组数据的方差是66
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com