
分析 (1)设徒弟单独做需要x天,那么师傅单独完成为$\frac{2}{3}$x天,根据现由徒弟先做4天,师徒再合作2天完成可列方程求解.
(2)根据工作量分报酬即可,看看师傅完成了工作量的多少就获得多少报酬,进而求得徒弟的.
解答 解:(1)设徒弟单独完成需要x天,则师傅需要$\frac{2}{3}$x天,根据题意可得:
4×$\frac{1}{x}$+2($\frac{1}{x}$+$\frac{1}{\frac{2}{3}x}$)=1,
解得:x=9,
检验得:x=9是原方程的根,
则$\frac{2}{3}$×9=6,
答:徒弟单独完成需要9天,则师傅需要6天;
(2)720×$\frac{1}{9}$×6=480(元),
720-480=240(元).
答:师傅得240元,徒弟是480元.
点评 本题考查分式方程的应用,根据工作量=工作时间×工作效率,完成工作的工作量为1,然后可列方程求解,进而根据个人完成的工作量求出报酬.


科目:初中数学 来源: 题型:解答题
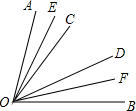 如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.
如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com