
【题目】某地发生8.1级地震,震源深度20千米.救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
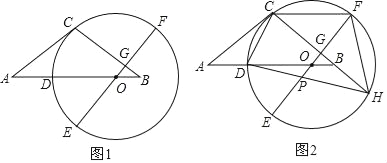
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
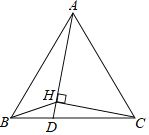
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
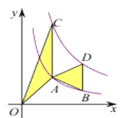
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则
,则![]() 的值为( )
的值为( )
A. 3 B. 4 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
(1)判断直线PC与⊙O的位置关系,并说明理由.
(2)若AB=5![]() ,BC=10,求⊙O的半径及PC的长.
,BC=10,求⊙O的半径及PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
(1)直接写出D,E两点的坐标,D( ),E( ),直接判断四边形NMPE的形状为 ;
(2)当t为何值时,四边形NMPE是正方形?
(3)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com