
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
(1)直接写出D,E两点的坐标,D( ),E( ),直接判断四边形NMPE的形状为 ;
(2)当t为何值时,四边形NMPE是正方形?
(3)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.

【答案】(1)(0,![]() ),(2,4),矩形;(2)t=
),(2,4),矩形;(2)t=![]() ;(3)t=
;(3)t=![]() 或t=2
或t=2![]() .
.
【解析】
(1)根据折叠的性质可知:AE=OA,OD=DE,那么可在直角三角形ABE中,用勾股定理求出BE的长,进而可求出CE的长,也就得出了E点的坐标.在直角三角形CDE中,CE长已经求出,CD=OC﹣OD=4﹣OD,DE=OD,用勾股定理即可求出OD的长,也就求出了D点的坐标;
(2)根据四边形PMNE是个矩形,可用时间t表示出AP,PE的长,然后根据相似三角形APM和AED求出PM的长,根据正方形的性质列方程即可得到结论;
(3)本题要分三种情况进行讨论:(Ⅰ)ME=MA时,此时MP为三角形ADE的中位线,那么AP=![]() ,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.
,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.
(Ⅱ)当MA=AE时,先在直角三角形OAD中求出斜边AD的长,然后根据相似三角形AMP和ADE来求出AP,MP的长,也就能求出t的值.根据折叠的性质,此时AF=AP,MF=MP,也就求出了M的坐标;
(Ⅲ)EM=EA的情况不成立.
解:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∵在Rt△ABE中,AE=AO=5,AB=4,BE=![]() =3,
=3,
∴CE=2,
∴E点坐标为(2,4),
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(4﹣OD)2+22=OD2,
解得:OD=![]() .
.
∴D点坐标为(0,![]() ).
).
∵PM∥DE,MN∥EP,
∴四边形NMPE为平行四边形.
又∵∠DEA=90°,
∴四边形PMNE为矩形;
故答案为:(0,![]() ),(2,4),矩形;
),(2,4),矩形;
(2)∵PM∥ED,
∴△APM∽△AED.
∴![]() =
=![]() ,
,
∴PM=![]() .
.
又∵AP=t,ED=![]() ,AE=5,
,AE=5,
∴PM=![]() =
=![]() ,
,
当PM=PE时,四边形NMPE是正方形,
即![]() =5﹣t,
=5﹣t,
解得:t=![]() ,
,
当t=![]() 时,四边形NMPE是正方形;
时,四边形NMPE是正方形;
(3)(Ⅰ)若以AE为等腰三角形的底,则ME=MA(如图①)
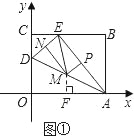
在Rt△AED中,ME=MA,
∵PM⊥AE,
∴P为AE的中点,
∴t=AP=![]() AE=
AE=![]() ,
,
又∵PM∥ED,
∴M为AD的中点,
过点M作MF⊥OA,垂足为F,则MF是△OAD的中位线,
∴MF=![]() OD=
OD=![]() ,OF=
,OF=![]() OA=
OA=![]() ,
,
∴当t=![]() 时,(0<
时,(0<![]() <5),△AME为等腰三角形,
<5),△AME为等腰三角形,
此时M点坐标为(![]() ,
,![]() );
);
(Ⅱ)若以AE为等腰三角形的腰,则AM=AE=5(如图②)
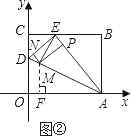
在Rt△AOD中,AD=![]() =
=![]() =
=![]() ,
,
过点M作MF⊥OA,垂足为F,
∵PM∥ED,
∴△APM∽△AED,
∴![]() ,
,
∴t=AP=![]() ,
,
∴PM=![]() t=
t=![]() ,
,
∴MF=MP=![]() ,OF=OA﹣AF=OA﹣AP=5﹣2
,OF=OA﹣AF=OA﹣AP=5﹣2![]() ,
,
∴当t=2![]() 时,(0<2
时,(0<2![]() <5),此时M点坐标为(5﹣2
<5),此时M点坐标为(5﹣2![]() ,
,![]() )
)
(Ⅲ)根据图形可知EM=EA的情况不成立,
综合综上所述,当t=![]() 或t=2
或t=2![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(![]() ,
,![]() )或(5﹣2
)或(5﹣2![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某地发生8.1级地震,震源深度20千米.救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P在斜边AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF.随着P点在边AB上位置的改变,EF的长度是否也会改变?若不变,请你求EF的长度;若有变化,请你求EF的变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,作出边长为1的菱形ABCD,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…按此规律所作的第2017个菱形的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m2=0.
(1)求证:不论m取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求该方程的另一根。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:

①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
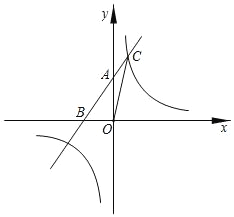
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
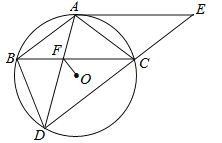
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com