
����Ŀ��ij�̳�Ϊ�������˿ͣ������һ�ִ��������һ�����������������4����ͬ��С�����Ϸֱ���С�0Ԫ������10Ԫ������20Ԫ���͡�30Ԫ�����������涨���˿��ڱ��̳�ͬһ���ڣ�ÿ������200Ԫ���Ϳ������������Ⱥ�����������һ�������Żأ����̳�������С��������ĺͷ�����Ӧ�۸�Ĺ���ȯ�����������ڱ��̳����ѣ�ij�˿պ�����200Ԫ��
��1���ù˿����ٿɵõ� Ԫ����ȯ������ɵõ� Ԫ����ȯ��
��2�������û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����30Ԫ�ĸ��ʣ�
���𰸡���1��10��50����2��![]()
���������⣺��1��10��50��
��2������״ͼ:
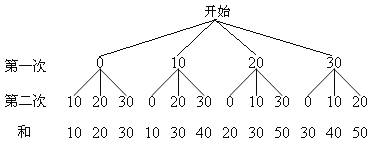
����ͼ���Կ���,����12�ֵȿ��ܽ��,���д��ڻ����30Ԫ����8�ֿ��ܽ��,
���P(������30Ԫ)��![]() ��
��
��1���������0Ԫ��10Ԫ��ʱ�õ��Ĺ���ȯ�����٣�һ��10Ԫ���������20Ԫ��30Ԫ��ʱ�õ��Ĺ���ȯ��࣬һ����50Ԫ��
��2���б�������״ͼ�����Բ��ظ�����©���г����п��ܵĽ�������ݸ��ʵ��������㣺��ȫ���ȿ�������������������������������Ŀ�����ߵı�ֵ�����䷢���ĸ��ʡ�


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
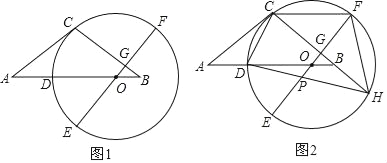
����Ŀ����ͼ1��������ABC�У�AC=BC����O��AB���ϣ���OΪԲ�ĵ�Բ������C����AB���ڵ�D��EFΪ��O��ֱ����EF��BC�ڵ�G����D��![]() ���е㣮
���е㣮
��1����֤��AC�ǡ�O�����ߣ�
��2����ͼ2���ӳ�CB����O�ڵ�H������HD��OE�ڵ�P������CF����֤��CF=DO+OP��
��3���ڣ�2���������£�����CD����tan��HDC=![]() ��CG=4����OP�ij���
��CG=4����OP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����O�����ߣ��е�ΪA��AB����O���ң�����B��BC��AD������O�ڵ�C������AC������C��CD��AB����AD�ڵ�D������AO���ӳ���BC�ڵ�M��������C��ֱ���ڵ�P���ҡ�BCP����ACD��
��1���ж�ֱ��PC����O��λ�ù�ϵ����˵�����ɣ�
��2����AB��5![]() ��BC��10������O�İ뾶��PC�ij���
��BC��10������O�İ뾶��PC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
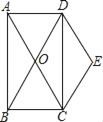
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O����DE��AC��CE��BD��
��1����֤���ı���OCED�����Σ�
��2������BAC=30�㣬AC=4��������OCED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼Ҷ������۾��еط���ɫ��ij����Ʒ��ÿ������Ϊ40Ԫ�������г�������һ�ܵ�������y�������۵���x��x��50��Ԫ/���Ĺ�ϵ���±���

��1��ֱ��д��y��x�ĺ�����ϵʽ��
��2����һ�ܵ���������ΪSԪ�������S��x�ĺ�����ϵʽ����ȷ�������۵�����ʲô��Χ�ڱ仯ʱ��һ�ܵ����������������۵��۵����������
��3���Ű�����ǣ����������������̼Ҿ�������Ʒһ�ܵ���������ȫ���������������̼ҹ�������Ʒ�Ļ������10000Ԫ�����������������̼�����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ���ǣ�������
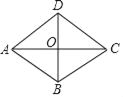
A. ��AB��BCʱ��ƽ���ı���ABCD������
B. ��AC��BDʱ��ƽ���ı���ABCD������
C. ��AC��BDʱ��ƽ���ı���ABCD��������
D. ����ABC��90��ʱ��ƽ���ı���ABCD�Ǿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA��5��OC��4����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������AE����һ����P������A��E�غϣ���A����AE������E�������˶����˶����ٶ�Ϊÿ��1����λ���ȣ����˶���ʱ��Ϊt�루0��t��5������P����ED��ƽ���߽�AD�ڵ�M������M��AE��ƽ���߽�DE�ڵ�N��
��1��ֱ��д��D��E��������꣬D���� ������E���� ������ֱ���ж��ı���NMPE����״Ϊ�� ����
��2����tΪ��ֵʱ���ı���NMPE�������Σ�
��3����tΪ��ֵʱ����A��M��EΪ�����������Ϊ���������Σ��������Ӧ��ʱ�̵�M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬BC=6��AC=8����P��Q����б��AB�ϵĶ��㣬��P��B ��A�˶��������B�غϣ�����Q��A��B�˶���BP=AQ����D��E�ֱ��ǵ�A��B��Q��PΪ�Գ����ĵĶԳƵ㣬 HQ��AB��Q����AC�ڵ�H������E���ﶥ��Aʱ��P��Qͬʱֹͣ�˶�����BP�ij�Ϊx����HDE�����Ϊy��
��1����֤����DHQ�ס�ABC��
��2����y����x�ĺ�������ʽ����y�����ֵ��
��3����xΪ��ֵʱ����HDEΪ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��2mx+m2��3��m�dz�������
��1��֤��������mȡʲôʵ��������������x�ᶼ������������
��2���������ߵĶ���ΪA����x����������ֱ�ΪB��D��B��D���Ҳ�����y��Ľ���ΪC��
����֤����mȡ��ֵͬʱ����ABD���ǵȱ���������
����|m|��![]() ��m��0ʱ����ABC������Ƿ������ֵ�����������������ֵ�����û������˵��������
��m��0ʱ����ABC������Ƿ������ֵ�����������������ֵ�����û������˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com