
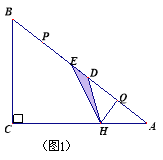
【题目】如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
【答案】
(1)略
(2)![]()
(3)当x的值为![]() 时,△HDE是等腰三角形
时,△HDE是等腰三角形
【解析】(14分)
(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴![]() =90°,HD=HA,
=90°,HD=HA,
∴![]() ,…………………………………………………………………………3分
,…………………………………………………………………………3分
∴△DHQ∽△ABC. ……………………………………………………………………1分
(2)①如图1,当![]() 时,
时,
ED=![]() ,QH=
,QH=![]() ,
,
此时![]() . …………………………………………3分
. …………………………………………3分
当![]() 时,最大值
时,最大值![]() .
.
②如图2,当![]() 时,
时,
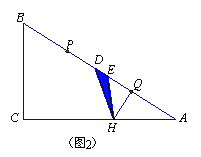
ED=![]() ,QH=
,QH=![]() ,
,
此时![]() . …………………………………………2分
. …………………………………………2分
当![]() 时,最大值
时,最大值![]() .
.
∴y与x之间的函数解析式为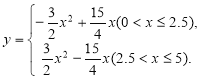
y的最大值是![]() .……………………………………………………………………1分
.……………………………………………………………………1分
(3)①如图1,当![]() 时,
时,
若DE=DH,∵DH=AH=![]() , DE=
, DE=![]() ,
,
∴![]() =
=![]() ,
,![]() .
.
显然ED=EH,HD=HE不可能; ……………………………………………………1分
②如图2,当![]() 时,
时,
若DE=DH,![]() =
=![]() ,
,![]() ; …………………………………………1分
; …………………………………………1分
若HD=HE,此时点D,E分别与点B,A重合,![]() ; ………………………1分
; ………………………1分
若ED=EH,则△EDH∽△HDA,
∴![]() ,
,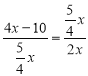 ,
,![]() . ……………………………………1分
. ……………………………………1分
∴当x的值为![]() 时,△HDE是等腰三角形.
时,△HDE是等腰三角形.
(其他解法相应给分)


科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m2=0.
(1)求证:不论m取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求该方程的另一根。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:

①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
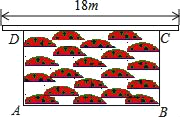
【题目】2018年,汶上县县委、县政府启动创建全国卫生县城和全国文明县城工作,各单位都积极投身创城工作某单位为进一步美化我县环境,在临街的围墙外靠墙摆设一长方形花圃景观,花圃一边靠墙,墙长18m,外围用40m的栅栏围成,如图所示,若设花圃的BC边长为x(m),花圃的面积为y(m2).
(1)求出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)利用所学知识试着求出花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
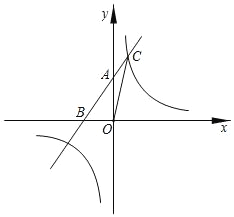
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
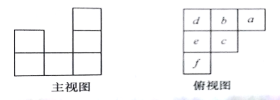
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com