
【题目】某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:

(1)直接写出y与x的函数关系式:
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的货款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
【答案】(1)y=﹣10x+1000,(x≥50);(2)S==﹣10x2+1400x﹣40000,当50<x<70时,销售利润随着销售单价的增大而增大;(3)8750.
【解析】
由图表可知,y与x满足一次函数关系,设y=kx+b,将表格中的两组数据代入得,![]() ,②-①得,10k=-100,解得k=-10,将k=-10代入①得,b=1000,故y=-10x+1000.
,②-①得,10k=-100,解得k=-10,将k=-10代入①得,b=1000,故y=-10x+1000.
根据利润等于售价减去进价即可求出S与x的函数关系式,再根据二次函数的性质即可求出一周的销售利润随着销售单价的增大而增大时,销售单价的范围.
根据当x≥70时,一周的销售利润随着销售单价的增大而减小,将x=75代入(2)中的关系式求解即可.
(1)设y=kx+b,由题意得:![]() ,解得:
,解得:![]() ,则函数关系式为:y=﹣10x+1000,(x≥50)
,则函数关系式为:y=﹣10x+1000,(x≥50)
(2)由题意得:S=(x﹣40)y=(x﹣40)(﹣10x+1000)
=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000.
∵﹣10<0,∴函数图象开口向下,对称轴为直线x=70,∴当50<x<70时,销售利润随着销售单价的增大而增大;
(3)∵由40(﹣10x+1000)≤10000
解得x≥75
又由于最大进货量为:y=10000÷40=250
由题意可知,当x=75时,可以销售250件商品,结合图形,故此时利润最大.
S=250×(75﹣40)=8750(元)
故该商家在10000元内的进货条件下,最大捐款为8750元.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
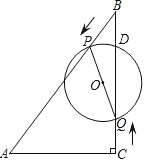
【题目】如图,在 Rt△ABC 中,∠ACB=90°,AC=6cm,∠ABC=30°,动点 P 从点 B 出发,在 BA 边上以每秒 2cm 的速度向点 A 匀速运动,同时动点 Q 从点 C 出发,在 CB 边上以每秒![]() cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
(1)当 t=1 时,求△BPQ 的面积;
(2)设⊙O 的面积为 y,求 y 与 t 的函数解析式;
(3)若⊙O 与 Rt△ABC 的一条边相切,求 t 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
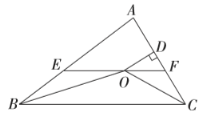
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,某班学生在一次数学活动课中,探索出如下结论,其中错误的是( )
,某班学生在一次数学活动课中,探索出如下结论,其中错误的是( )
A.![]() B.点
B.点![]() 到
到![]() 各边的距离相等
各边的距离相等
C.![]() D.设
D.设![]() ,
,![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P在斜边AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF.随着P点在边AB上位置的改变,EF的长度是否也会改变?若不变,请你求EF的长度;若有变化,请你求EF的变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
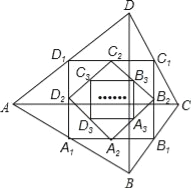
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,作出边长为1的菱形ABCD,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…按此规律所作的第2017个菱形的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:

①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
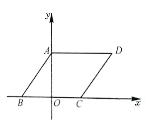
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA,OB的长是关于x的一元二次方程![]() 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)若点E为x轴上的点,且△AOE的面积为![]() .
.
求:①点E的坐标;②证明:△AOE∽△DAO;
(2)若点M在平面直角坐标系中,则在直线AB上是否存在点F,使以A,C,F,M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com