
【题目】已知抛物线y=a(x-h)2+k的对称轴是直线x=3,经过点(1,-2)和点(2,1).
(1)求函数的解析式;
(2)若m<n<3,A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
【答案】(1)y=-(x-3)2+2;(2)y1<y2.
【解析】
(1)设抛物线y=a(x-h)2+k,根据对称轴是直线x=3,求得 h=3,把点(1,-2)和点(2,1)带入y=a(x-3)2+k中求出a与k的值即可;(2)根据对称轴判断A、B的位置,挺好利用抛物线的增减性判断![]() 的大小.
的大小.
(1)抛物线y=a(x-h)2+k的对称轴是直线x=3,∴h=3
把点(1,-2)和点(2,1)带入y=a(x-3)2+k中
-2=a(1-3)2+k,1=a(2-3)2+k
解得a=-1,k=2
y=-(x-3)2+2;
(2)∵函数y=-(x-3)2+2的对称轴为x=3,
![]() 、
、![]() 在对称轴左侧,
在对称轴左侧,
又∵抛物线开口向下,
∴对称轴左侧y随x的增大而增大,
∵m<n<3 ![]()


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )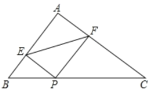
A. 2B. 2.4C. 2.5D. 2.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
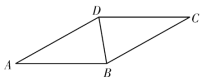
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.
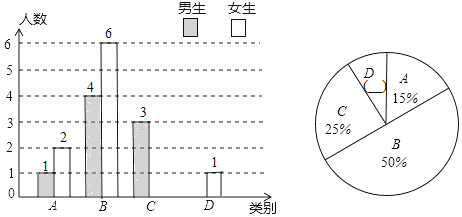
请根据统计图解答下列问题:
(1)本次调查中,杨老师一共调查了 名学生,其中C类女生有 名,D类男生有 名;
(2)补全上面的条形统计图和扇形统计图;
(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )
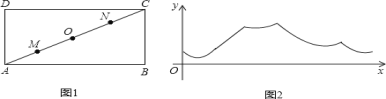
A. D点B. M点C. O点D. N点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角角形的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.

证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com