
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角角形的周长
【答案】(1)证明见解析;
(2)方程的另一根为2,围成直角三角形的周长为3+![]() .
.
【解析】
(1)由根的判别式△=(m-2)2≥0,可证出:不论m为何值,该方程总有两个实数根;
(2)将x=1代入原方程可求出m的值,利用两根之积等于![]() 可求出方程的另一个根,再利用勾股定理及三角形的周长公式即可求出围成直角三角形的周长.
可求出方程的另一个根,再利用勾股定理及三角形的周长公式即可求出围成直角三角形的周长.
(1)证明:△=[﹣(m+2)]2﹣4×1×2m=m2﹣4m+4=(m﹣2)2.
∵(m﹣2)2≥0,即△≥0,
∴不论m为何值,该方程总有两个实数根.
(2)解:将x=1代入原方程,得:1﹣(m+2)+2m=0,
∴m=1,
∴方程的另一根为![]() =2.
=2.
∵![]() =
=![]() ,
,
∴围成直角三角形的周长=1+2+![]() =3+
=3+![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,小李从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2m,现己知购买这种铁皮每平方米需30元钱,问小李购回这张矩形铁皮共花了多少元钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a![]() 0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2
0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2![]() x1<x2<4.
x1<x2<4.
其中结论正确的有( )
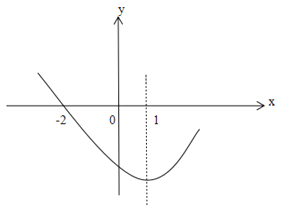
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x-h)2+k的对称轴是直线x=3,经过点(1,-2)和点(2,1).
(1)求函数的解析式;
(2)若m<n<3,A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,对角线AC、BD长分别为16、12,折叠纸片使点A落在DB上,折痕交AC于点P,则DP的长为( )
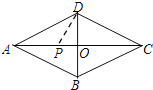
A. 3![]() B.
B. ![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别在矩形ABCD的边AD、AB上,连接EF,四边形ABFE沿EF翻折能与四边形![]() 重合,且
重合,且![]() 与ED相交,若
与ED相交,若![]() ,则
,则![]()
![]()
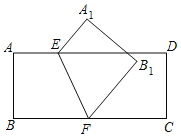
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
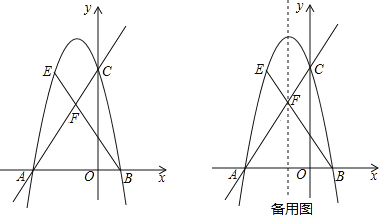
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
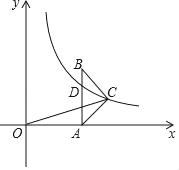
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com