
����Ŀ����ͼ�����κ���y=ax2+bx+c��a![]() 0����ͼ����㣨-2,0�����Գ���Ϊֱ��x=1.�����½��ۣ���abc>0����8a+c>0������A��x1��m����B��x2��m�����������ϵ����㣬��x=x1+x2ʱ��y=c����������a��x+2����4-x��=-2������Ϊx1��x2����x1<x2����-2
0����ͼ����㣨-2,0�����Գ���Ϊֱ��x=1.�����½��ۣ���abc>0����8a+c>0������A��x1��m����B��x2��m�����������ϵ����㣬��x=x1+x2ʱ��y=c����������a��x+2����4-x��=-2������Ϊx1��x2����x1<x2����-2![]() x1<x2<4.
x1<x2<4.
���н�����ȷ���У� ��
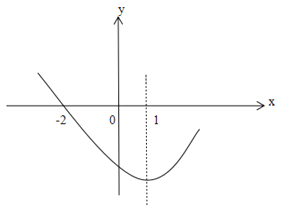
A. 1��B. 2��C. 3��D. 4��
���𰸡�B
��������
���ݶ��κ�����ͼ�������ʼ�������𰸣�
![]() �����߿������ϣ�
�����߿������ϣ�![]() a>0.
a>0.
![]() �����ߵĶԳ�����y���Ҳ࣬
�����ߵĶԳ�����y���Ҳ࣬![]() a��b��ţ�
a��b��ţ�![]() b<0.
b<0.
![]() �����߽�y���ڸ����ᣬ
�����߽�y���ڸ����ᣬ![]() c<0��
c<0��![]() abc>0��
abc>0��![]() ����ȷ.
����ȷ.
![]() �����ߵĶԳ���Ϊx=1��
�����ߵĶԳ���Ϊx=1��![]()
![]() =1��
=1��![]() b=-2a.
b=-2a.
��x=-2ʱ��4a-2b+c=0��![]() 4a+4a+c=0����8a+c=0��
4a+4a+c=0����8a+c=0��![]() �ڴ���.
�ڴ���.
![]() A��x1��m����B��x2��m�����������ϵ����㣬���������ߵĶԳ��ԣ�
A��x1��m����B��x2��m�����������ϵ����㣬���������ߵĶԳ��ԣ�![]() x1+x2=1��2=2��
x1+x2=1��2=2��
![]() ��x=x1+x2ʱ����x=2ʱ��y=4a+2b+c=4a-4a+c=c��
��x=x1+x2ʱ����x=2ʱ��y=4a+2b+c=4a-4a+c=c��![]() ����ȷ.
����ȷ.
![]() �����ߵĶԳ���Ϊx=1������x���һ������Ϊ��-2��0����
�����ߵĶԳ���Ϊx=1������x���һ������Ϊ��-2��0����
![]() ��x�����һ������Ϊ��4��0����
��x�����һ������Ϊ��4��0����![]() ԭ����Ϊ��y=a��x+2����x-4��.
ԭ����Ϊ��y=a��x+2����x-4��.
������a��x+2����4-x��=-2��������a��x+2����x-4��=2������Ϊx1��x2����x1��x2Ϊ��������ֱ��y=2����������ĺ�����.
��![]() x1<x2����x1<-2<4<x2��
x1<x2����x1<-2<4<x2��![]() �ܴ���.
�ܴ���.
������������ȷ�Ľ�����2��.
��ѡB.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ����ɫ��������������٣�ij�����ƻ���ֲ�ס������ֻ���������С������������ֲ���ֻ���![]() �����ֻ���
�����ֻ���![]() ������430Ԫ����ֲ���ֻ���
������430Ԫ����ֲ���ֻ���![]() �����ֻ���
�����ֻ���![]() ������260Ԫ��
������260Ԫ��
��1����������ֲ���ֻ���![]() ����ֲ���ֻ���
����ֲ���ֻ���![]() �������Ԫ��
�������Ԫ��
��2������������ֲ���ֻ��ܹ�![]() �ҷ��ò�����6300Ԫ����ô�����������ֲ���ֻ��ܶ���ƽ���ף�
�ҷ��ò�����6300Ԫ����ô�����������ֲ���ֻ��ܶ���ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�·ݵ�Ӫҵ��Ϊ200��Ԫ��һ�¡����¡����µ�Ӫҵ�1000��Ԫ�����ƽ��ÿ��������Ϊ![]() �����������з���ӦΪ____________________________ ��
�����������з���ӦΪ____________________________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,BD ������ABCD �ĶԽ���,��A��30����
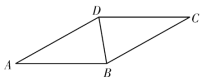
(1)���ó߹���ͼ��,��AB �Ĵ�ֱƽ����EF,����ΪE,��AD ��F;(��Ҫ ��д����,������ͼ�ۼ�)
(2)��(1)��������,����BF,���DBF �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������ƽ����Ϊ
������ʵ������ƽ����Ϊ![]() ����ô
����ô![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A. 5 B. -1 C. 5��-1 D. -5��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ���˽����̰༶ѧ���κ�ϰ�ľ���������Ա��ಿ��ѧ��������һ���µĸ��ٵ��飬Ȼ�������ֳ����ࣺA�����㣻B�����ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ��
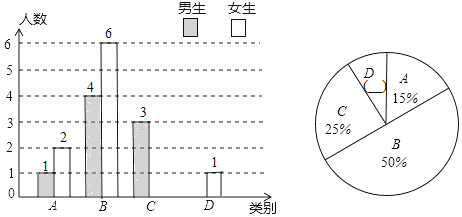
�����ͳ��ͼ����������⣺
��1�����ε����У�����ʦһ���������� ����ѧ��������C��Ů������ ������D���������� ������
��2����ȫ���������ͳ��ͼ������ͳ��ͼ��
��3���ڴ˴ε����У�Сƽ����D�࣮Ϊ�˽�������������ʦ�ӱ������A��ѧ�������ѡȡһλͬѧ������������һ��һ���Ŀκ���ѧϰ���������ѡ��ͬѧǡ����һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��������,С��ÿ�����ϼ������С�������ľ��ι�ABCD��ϰ�ܲ�,�ְ�վ�ڵ�ijһ���̶��㴦������м�ʱָ��������С���ھ��ι�ABCD�ı�������A��B��C��D��A�ķ����ܲ�һ��,С���ܲ���·��Ϊx��,С����ְ�֮��ľ���Ϊy��.y��x֮��ĺ�����ϵ��ͼ2��ʾ,��ְ����ڵ�λ�ÿ���Ϊͼ1��( )
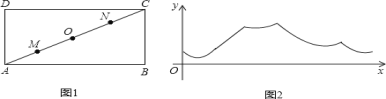
A. D��B. M��C. O��D. N��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����m+2��x+2m��0
��1����֤������mΪ��ֵ���÷�����������ʵ������
��2�����˷��̵�һ������1����������̵���һ������������Դ�����Ϊ�߳���ֱ�ǽ��ε��ܳ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��ͼ����ͼ��ʾ������ͼ�����������⣺
��1����������x�����һ���������ꣻ�� ����
��2������ax2+bx+c=0������������ ����
��3������ʽax2+bx+c��0�Ľ����� ����
��4��y��x���������С���Ա���x��ȡֵ��Χ���� ����
��5����������ߵĽ���ʽ���������꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com