
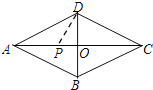
【题目】如图,在菱形纸片ABCD中,对角线AC、BD长分别为16、12,折叠纸片使点A落在DB上,折痕交AC于点P,则DP的长为( )
A. 3![]() B.
B. ![]() C. 3
C. 3![]() D. 3
D. 3![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形。

(1)求证AE=CG,并说明理由。
(2)连接AG,若AB=17,DG=13,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )
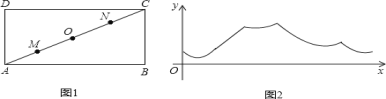
A. D点B. M点C. O点D. N点
查看答案和解析>>
科目:初中数学 来源: 题型:
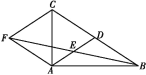
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角角形的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
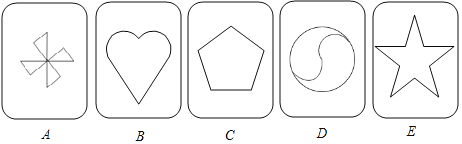
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
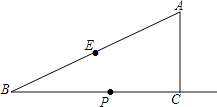
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com