
如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.

解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴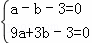 ,
,
解得: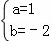 ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3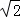 ,BM=2
,BM=2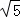 ,CM=
,CM=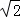 ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)如图1,
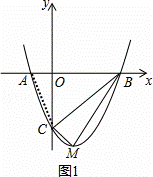
连接AC,
∵△COA∽△CAP,△PCA∽△BCD,
∴Rt△COA∽Rt△BCD,P点与O点重合,
∴点P(0,0).
如图2,过A作AP1⊥AC交y轴正半轴于P1,
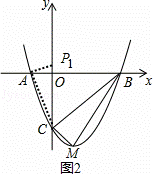
∵Rt△CAP1∽Rt△COA∽Rt△BCD,
∴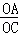 =
=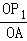 ,
,
即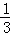 =
=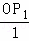 ,
,
∴点P1(0,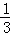 ).
).
如图3,过C作CP2⊥AC交x轴正半轴于P2,
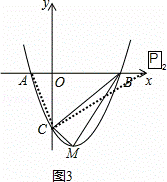
∵Rt△P2CA∽Rt△COA∽Rt△BCD,
∴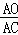 =
=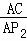 ,
,
即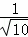 =
=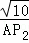 ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,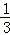 ),P2(9,0).
),P2(9,0).
点评: 此题是二次函数的综合题,涉及到二次函数解析式的确定、勾股定理、直角三角形的判定、相似三角形的判定和性质等知识,(3)题中能够发现点O是符合要求的P点,是解决此题的突破口.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )
A.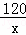 =
=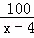 B.
B. 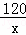 =
=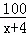 C.
C. 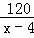 =
=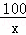 D.
D. 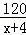 =
=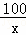
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: ≈1.41,
≈1.41, ≈1.73.
≈1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件为必然事件的是( )
A.经过有交通信号灯的路口,遇到红灯
B.明天一定会下雨
C.抛出的篮球会下落
D.任意买一张电影票,座位号是2的倍数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com