
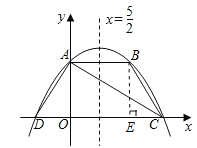
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=![]() ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )

A.点B坐标为(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
【答案】D
【解析】
由抛物线y=ax2+bx+4交y轴于点A,可得点A的坐标,然后由抛物线的对称性可得点B的坐标,由点B关于直线AC的对称点恰好落在线段OC上,可知∠ACO=∠ACB,再结合平行线的性质可判断∠BAC=∠ACB,从而可知AB=AD;过点B作BE⊥x轴于点E,由勾股定理可得EC的长,则点C坐标可得,然后由对称性可得点D的坐标,则OCOD的值可计算;由勾股定理可得AD的长,由交点式可得抛物线的解析式,根据以上计算或推理,对各个选项作出分析即可.
解:因为抛物线y=ax2+bx+4交y轴于点A,所以A(0,4).因为对称轴为直线x=![]() ,AB∥x轴,所以B(5,4),选项A正确,不符合题意.如答图,过点B作BE⊥x轴于点E,则BE=4,AB=5.因为AB∥x轴,所以∠BAC=∠ACO.因为点B关于直线AC的对称点恰好落在线段OC上,所以∠ACO=∠ACB,所以∠BAC=∠ACB,所以BC=AB=5.在Rt△BCE中,由勾股定理得EC=3,所以C(8,0),因为对称轴为直线x=
,AB∥x轴,所以B(5,4),选项A正确,不符合题意.如答图,过点B作BE⊥x轴于点E,则BE=4,AB=5.因为AB∥x轴,所以∠BAC=∠ACO.因为点B关于直线AC的对称点恰好落在线段OC上,所以∠ACO=∠ACB,所以∠BAC=∠ACB,所以BC=AB=5.在Rt△BCE中,由勾股定理得EC=3,所以C(8,0),因为对称轴为直线x=![]() ,所以D(-3,0).在Rt△ADO中,OA=4,OD=3,所以AD=5,所以AB=AD,选项B正确,不符合题意.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入得4=a(0+3)(0-8),解得a=
,所以D(-3,0).在Rt△ADO中,OA=4,OD=3,所以AD=5,所以AB=AD,选项B正确,不符合题意.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入得4=a(0+3)(0-8),解得a=![]() ,选项C正确,不符合题意.因为OC=8,OD=3,所以OCOD=24,选项D错误,符合题意,因此本题选D.
,选项C正确,不符合题意.因为OC=8,OD=3,所以OCOD=24,选项D错误,符合题意,因此本题选D.


科目:初中数学 来源: 题型:
【题目】某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元
(1)求每台A型加湿器和B型加湿器的销售利润;
(2)该商店计划一次购进两种型号的加湿器共100台,其中B型加湿器的进货量不超过A型加湿器的2倍,设购进A型加湿器x台.这100台加湿器的销售总利润为y元
①求y关于x的函数关系式;
②该商店应怎样进货才能使销售总利润最大?
(3)实际进货时,厂家对A型加湿器出厂价下调m(0<m<100)元,且限定商店最多购进A型加湿器70台,若商店保持两种加湿器的售价不变,请你根据以上信息及(2)中条件,设计出使这100台加湿器销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
类别 | 频数(人数) | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
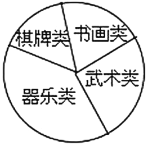
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:
①![]() ____,
____,![]() _____;
_____;
②在扇形统计图中,器乐类所对应扇形的圆心角是_____度;
③若该校七年级有学生460人,请你估计大约有多少学生参加武术类校本课程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象交于A,B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C,设二次函数图象的顶点为D.
的图象交于A,B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C,设二次函数图象的顶点为D.
(1)求点C的坐标;
(2)若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的解析式;
(3)若![]() ,且△ACD的面积等于10,请直接写出满足条件的点D的坐标.
,且△ACD的面积等于10,请直接写出满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
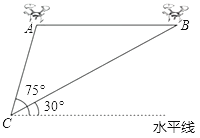
【题目】某测绘公司借助大型无人飞机航拍测绘.如图,无人飞机从C处放飞迅速爬升到点A处,继续水平飞行400米到达B处共需150秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.己知无人飞机的水平飞行速度为4米/秒,求这架无人飞机从C到A的爬升速度及水平飞行高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水产养殖户开发一个三角形状的养殖区域,A、B、C三点的位置如图所示.已知∠CAB=105°,∠B=45°,AB=100![]() 米.(参考数据:
米.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
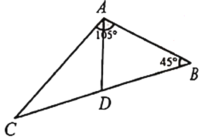
(1)求养殖区域△ABC的面积;
(2)养殖户计划在边BC上选一点D,修建垂钓栈道AD,测得∠CAD=40°,求垂钓栈道AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com