
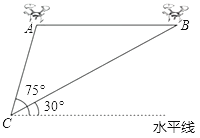
【题目】某测绘公司借助大型无人飞机航拍测绘.如图,无人飞机从C处放飞迅速爬升到点A处,继续水平飞行400米到达B处共需150秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.己知无人飞机的水平飞行速度为4米/秒,求这架无人飞机从C到A的爬升速度及水平飞行高度.(结果保留根号)
【答案】这架无人飞机从C到A的爬升速度为![]() 米/秒,水平飞行高度为(100+100
米/秒,水平飞行高度为(100+100![]() )米
)米
【解析】
如图,作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD、AC的长,由CD+BD求出BC的长,求出BH的长,根据路程、速度、时间的关系求得从C到A的爬升时间,即可求得爬升速度.
如图,作AD⊥BC,BH⊥水平线,
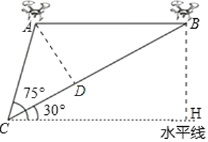
由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,
∴∠ABC=30°,∠ACB=45°,
∴△ADC为等腰直角三角形,
∵AB=400米,
∴AD=CD=ABsin30°=200(米),BD=ABcos30°=200![]() ,
,
∴AC=![]() AD=200
AD=200![]() ,BC=CD+BD=200+200
,BC=CD+BD=200+200![]() ,
,
∴BH=BCsin30°=100+100![]() (米),
(米),
从A飞行400米到达B处,所需时间为:![]() (秒),
(秒),
∴从C到A的爬升时间为:150-100=50(秒),
∴爬升速度为:![]() (米/秒),
(米/秒),
答:这架无人飞机从C到A的爬升速度为![]() 米/秒,水平飞行高度为(100+100
米/秒,水平飞行高度为(100+100![]() )米.
)米.


科目:初中数学 来源: 题型:
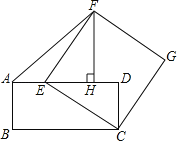
【题目】如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF,当AE为_____时,△AEF的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
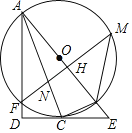
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初三300名学生每天做家庭作业的时间情况,从中随机抽取50名学生进行抽样调查,按做作业的时间t(单位:小时),将学生分成四类:A类(![]() ),B类(
),B类(![]() ),C类(
),C类(![]() ),D类(
),D类(![]() ),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:

(1)补全条形统计图,并估计初三学生做作业时间为D类的学生共有多少人?
(2)抽样调查的A类学生中有3名男生和1名女生,若从中任选2人,求这2人均是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=![]() ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )

A.点B坐标为(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
查看答案和解析>>
科目:初中数学 来源: 题型:
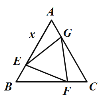
【题目】已知正![]() ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设
ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设![]() EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
A.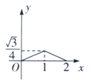 B.
B.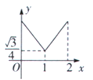 C.
C.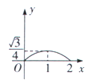 D.
D.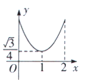
查看答案和解析>>
科目:初中数学 来源: 题型:
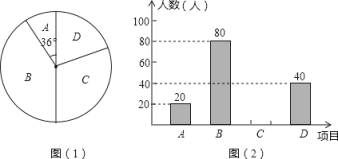
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有多少人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
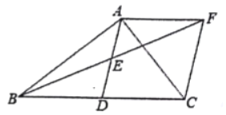
【题目】如图,在![]() 中,
中,![]() ,AD是BC边上的中线,点E为AD的中点,过点A作
,AD是BC边上的中线,点E为AD的中点,过点A作![]() 交BE的延长线于点F,连接CF.
交BE的延长线于点F,连接CF.
(1)求证:![]() ;
;
(2)连接DF,当![]() 度时,四边形ABDF为菱形?证明你的结论.
度时,四边形ABDF为菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com