
【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动 ![]() 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).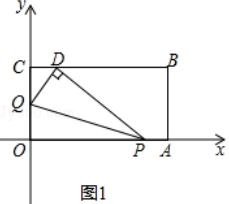
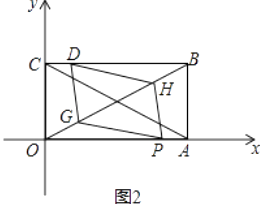
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形.
【答案】
(1)
解:∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点Q从O点以每秒1个单位长的速度沿OC向终点C运动,运动 ![]() 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.
∴当点P的运动时间为t(秒)时,
AP=t,OQ= ![]() +t,
+t,
则OP=OA﹣AP=6﹣t;
(2)
解:当t=1时,OQ= ![]() ,则CQ=CQ=OC﹣OQ=
,则CQ=CQ=OC﹣OQ= ![]() ,
,
由折叠可知:△OPQ≌△DPQ,
∴OQ=DQ= ![]() ,
,
由勾股定理,得:CD=1,
∴D(1,3);
(3)
证明:如图所示,
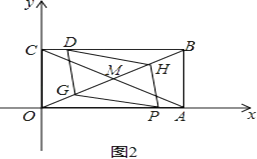
由(1),(2)知:当t=1时,
CD=AP=1,OA=BC=6
∴BC﹣CD=OA﹣AP,即BD=OP=5,
∵四边形OABC是矩形,
∴OM=MB,OA∥BC,
∵G为OM中点,H为BM中点,
∴OG=BH,
∵OA∥BC,
∴∠CBO=∠AOB,
在△POG和△DBH中,
∵  ,
,
∴△POG≌△DBH(SAS),
∴∠OGP=∠BHD,PG=DH,
∴∠MGP=∠DHM,
∴PG∥DH,
∵PG=DH,
∴四边形DGPH是平行四边形.
故当t=1时四边形DGPH是平行四边形.
【解析】(1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据P点与Q点的运动速度与运动时间即可用含t的代数式表示OP,OQ;(2)由翻折的性质可知:△OPQ≌△DPQ,进而可得:DQ=OQ,然后由t=1时,DQ=OQ= ![]() ,CQ=OC﹣OQ=
,CQ=OC﹣OQ= ![]() ,然后利用勾股定理可求CD的值,进而可求点D的坐标;(3)由(1),(2)知:当t=1时,CD=AP=1,OA=BC=6,进而可得:BD=OP=5,然后由矩形的性质可得:OG=BH,∠CBO=∠AOB,然后根据SAS证明△POG≌△DBH,进而可得PG∥DH,PG=DH,然后根据一组对边平行且相等的四边形是平行四边形,即可求证:当t=1时四边形DGPH是平行四边形.
,然后利用勾股定理可求CD的值,进而可求点D的坐标;(3)由(1),(2)知:当t=1时,CD=AP=1,OA=BC=6,进而可得:BD=OP=5,然后由矩形的性质可得:OG=BH,∠CBO=∠AOB,然后根据SAS证明△POG≌△DBH,进而可得PG∥DH,PG=DH,然后根据一组对边平行且相等的四边形是平行四边形,即可求证:当t=1时四边形DGPH是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )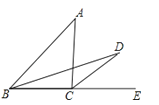
A.46°
B.92°
C.44°
D.23°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7名学生参加决赛,他们的决赛成绩各不相同,其中一名参赛选手想知道自己是否进前4名,他除了知道自己成绩外,还要知道这7名学生成绩的( )
A. 众数B. 方差C. 平均数D. 中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
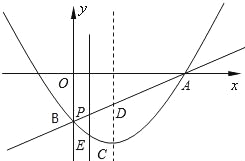
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com