

分析 (1)根据非负数的和为0的定理建立方程求出其解;
(2)根据A,B两点到原点O的距离相等分两种情况:当A、B在原点的左侧A、B相遇时和A、B在原点的异侧时,建立方程求出其解即可;
(3)第一次同时到达的点是A追上B的地方,第二次同时到达的点是A返回的过程中与A相遇的地方,第三次相遇是B在返回的过程中与A相遇的地方,第五次相遇是A追上B的地方,第六次相遇的A返回与B相遇的地方.
解答 解:(1)由题意,得
a+4=0,c-1=0,
解得:a=-4,c=1
答:a对应的数为-4,b对应的数为1;
(2)∵点B对应的数为-3,A对应的数是-4,
∴AB=1.AO=4,BO=3.
当A、B在原点的左侧A、B相遇时,
2t-t=1,
t=1,
当A、B在原点的异侧时,
2t-4=3-t,
解得:t=$\frac{7}{3}$.
∴A,B两点到原点O的距离相等时,t的值为1或$\frac{7}{3}$.
(3)由(2)得,
当t=1时,A,B两点同时到达的点是-2;
2.5秒时A点对应的数是1,B点对应的数是-0.5,
∴AB=1.5,
设过t秒A、B相遇,由题意得
2t+t=1.5,
解得:t=0.5,
此时A,B两点同时到达的点是0.
再过两秒时A到达A点,B返回在0,
∴AB=4,设A、B再过t秒相遇,由题意,得
2t+t=4,
t=$\frac{4}{3}$,
此时A,B两点同时到达的点是-$\frac{4}{3}$.在此3秒时,A为0,B为-3.
∴A,B两点同时到达的点在数轴上表示的数为:-2,0,-$\frac{4}{3}$.
点评 本题考查了一元一次方程的运用,数轴的运用,绝对值的运用,偶次幂的运用,解答时根据行程问题的追击问题和相遇问题的数量关系建立方程是关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
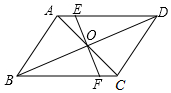 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
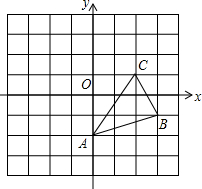 将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
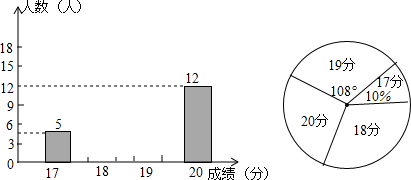
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com