
【题目】如图,平行四边形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,已知
轴上,已知![]() ,
,![]() ,
,![]() .
.

(1)平行四边形![]() 的面积为________;
的面积为________;
(2)如图1,点![]() 是
是![]() 边上的一点,若
边上的一点,若![]() 的面积是平行四边形
的面积是平行四边形![]() 的
的![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将![]() 绕点
绕点![]() 顺时针旋转,旋转得
顺时针旋转,旋转得![]() ,在整个旋转过程中,能否使以点
,在整个旋转过程中,能否使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若能,求点
为顶点的四边形是平行四边形?若能,求点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)32;(2)点E的坐标为(![]() ,2);(3)能,点A1的坐标为
,2);(3)能,点A1的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由题意可得AB=8,根据平行四边形的面积公式可求得ABCD的面积;
(2)过点E作EF⊥AB,根据△ABE的面积是ABCD的![]() ,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
(3)分以下三种情况讨论:①四边形OA1D1B是平行四边形,②四边形A1D1OB是平行四边形,③四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E.先分别画出示意图,利用旋转的性质,平行四边形的性质再结合面积法及勾股定理可分别得出点A1的坐标.
解:(1)∵OA=3,OB=5,OD=4.
∴AB=8,∴ABCD的面积=4×8=32,
故答案为:32;
(2)过点E作EF⊥AB于F,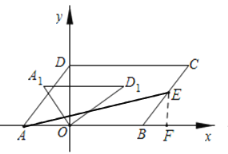
∵S△ABE=![]() SABCD,∴
SABCD,∴![]() ×AB×EF=
×AB×EF=![]() ×32,∴EF=2.
×32,∴EF=2.
∵OB=5,CD=AB=8,OD=4,
∴点B(5,0),点C(8,4),
设直线BC的解析式为y=kx+b,
![]() ,解得
,解得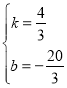 ,
,
∴直线BC的解析式为y=![]() ,
,
当y=2时,x=![]() ,
,
∴点E的坐标为(![]() ,2);
,2);
(3)能使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,理由如下:
为顶点的四边形是平行四边形,理由如下:
∵OA=3,OD=4,∴AD=5,分以下三种情况:
①如图,若四边形OA1D1B是平行四边形,A1D1交y轴于点F,
∵将△AOD绕点O顺时针旋转,旋转得△A1OD1,
∴A1O=AO=3,OD1=OD=4,∠A1OD1=∠AOD=90°.
∵四边形OA1D1B是平行四边形,
∴A1D1=BO=5,A1D1∥AB,∴∠A1FO=180°-∠AOD=90°,
∴S△A1OD1=![]() ×A1O×OD1=
×A1O×OD1=![]() ×A1D1×OF,
×A1D1×OF,
∴OF=![]() ,
,![]() ,
,
∵点A1在第二象限,∴A1的坐标为![]() ;
;
②如图,若四边形A1D1OB是平行四边形,A1D1交y轴于点F,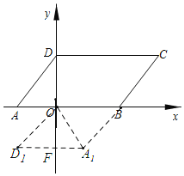
同①可得,![]() ,
,
∵点A1在第四象限,∴A1的坐标为![]() ;
;
③如图,若四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E,
∵OA1BD1是平行四边形,且∠A1OD1=90°,
∴四边形OA1BD1是矩形,∴OD1=A1B=4,∠OA1B=90°,
∵S△A1OB=![]() ×OB×A1E=
×OB×A1E=![]() ×A1O×A1B,
×A1O×A1B,
∴A1E=![]() ,∴OE=
,∴OE=![]() ,
,
∴A1的坐标为![]() .
.
综上所述,符合条件的点A1的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
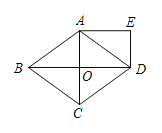
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为![]() 、
、![]() ,
,![]() ,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。
,若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A′B′C′,点A、B、C的对应点分别为A′、B′、C′。
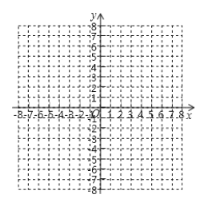
(1)写出点A′、B′、C′的坐标;
(2)在图中画出平移后的三角形A′B′C′;
(3)三角形A′B′C′的面积为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]()
![]() 在第一象限内的图像交于
在第一象限内的图像交于![]() 和
和![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)在第一象限内,当一次函数![]() 的值大于反比例函数
的值大于反比例函数![]()
![]() 的值时,写出自变量
的值时,写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
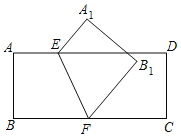
【题目】如图,点E、F分别在矩形ABCD的边AD、AB上,连接EF,四边形ABFE沿EF翻折能与四边形![]() 重合,且
重合,且![]() 与ED相交,若
与ED相交,若![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.
(1)求证:M与其“友谊数”的差能被15整除;
(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com