
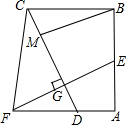
 已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )
已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )| A. | 只有①② | B. | 只有②③ | C. | 只有①③ | D. | ①②③ |
分析 ①不正确;证出△AEF是等腰直角三角形,得EF=$\sqrt{2}$AE,由题意得出D与A重合,△ABC是等腰直角三角形,得CD=$\sqrt{2}$AB,证出CD=2$\sqrt{2}$AE,得出CD=2EF,即可得出结论;
②正确;连接MF、ME,证明△MEG、△MEF是等腰直角三角形,得出EF=$\sqrt{2}$EM=$\sqrt{2}$FM=$\sqrt{2}$BM,得出BM=EM=FM,证出A、E、M、F四点共圆,由圆周角定理得出∠FAM=∠EAM,∠AFM=∠BEM=∠EBM,证出△AFM≌△ABM,即可得出结论;
③正确;连接DE,作EK∥BC交CD于K,则DK=CK,EK∥AF,证出EK=DF,设AD=1,则AE=2$\sqrt{2}$,由勾股定理求出DF=DE=3,得出EK=DF=3,证出EK是梯形ABCF的中位线,得出EK=$\frac{1}{2}$(AD+BC),求出BC=5,即可得出结果.
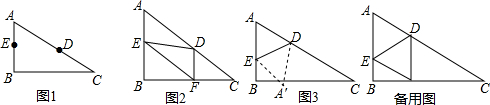
解答 解:①不正确;理由如下:如图1所示: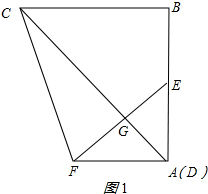
∵AF∥BC,∠ABC=90°,
∴∠BAF=90°,
∵AE=AF,
∴△AEF是等腰直角三角形,
∴EF=$\sqrt{2}$AE,
∵CD垂直平分EF于G,
∴D与A重合,
∴△ABC是等腰直角三角形,
∴CD=$\sqrt{2}$AB,
∵点E为AB的中点,
∴AB=2AE,
∴CD=2$\sqrt{2}$AE,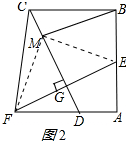
∴CD=2EF,
∴CD=EF不正确;
②正确;理由如下:
连接MF、ME,如图2所示:
∵CD垂直平分EF于G,
∴MF=ME,
∵MG=EG,
∴△MEG、△MEF是等腰直角三角形,
∴EF=$\sqrt{2}$EM=$\sqrt{2}$FM=$\sqrt{2}$BM,
∴BM=EM=FM,
∵∠EMF+∠BAF=180°,
∴A、E、M、F四点共圆,
∴∠FAM=∠EAM,∠AFM=∠BEM=∠EBM,
∴△AFM≌△ABM,
∴AB=AF;
③正确;理由如下:
连接DE,作EK∥BC交CD于K,如图3所示: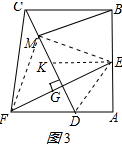
则DK=CK,EK∥AF,
∴EK:DF=EG:FG,
∵EG=FG,
∴EK=DF,
设AD=1,则AE=2$\sqrt{2}$,
∴DF=DE=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}$=3,
∴EK=DF=3,
∵EK是梯形ABCF的中位线,
∴EK=$\frac{1}{2}$(AD+BC),
∴BC=5,
∴BC=5AD.
正确的是②③,故选:B.
点评 本题是四边形综合题目,考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、勾股定理、四点共圆、圆周角定理、梯形中位线定理等知识;本题综合性强,难度较大,需要通过作辅助线才能得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
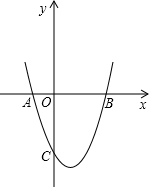 如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.
如图,二次函数y=x2+bx+c与坐标轴交于点A、B、C,且OB=OC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
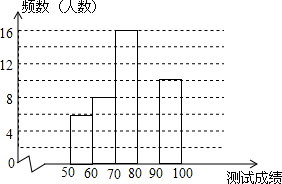 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写100个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com