
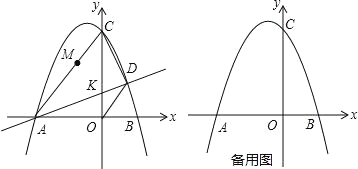
【题目】如图,抛物线![]() 与x轴交于点A、B(点A在点B的左侧)与y轴交于点C(0,8),点D是抛物线上的动点,直线AD与y轴交于点K.
与x轴交于点A、B(点A在点B的左侧)与y轴交于点C(0,8),点D是抛物线上的动点,直线AD与y轴交于点K.
(1)填空:c= ;
(2)若点D的横坐标为2,连接OD、CD、AC,以AC为直径作⊙M,试判断点D与⊙M的位置关系,并说明理由.
(3)在抛物线![]() 上是否存在点D,使得∠BAC=2∠BAD?若存在,试求出点D的坐标;若不存在,试说明理由.
上是否存在点D,使得∠BAC=2∠BAD?若存在,试求出点D的坐标;若不存在,试说明理由.
【答案】(1)8;(2)点D在⊙M上.理由见试题解析;(3)D的坐标为(2,4)或(![]() ).
).
【解析】
试题分析:(1)把C(0,8)代入抛物线y=﹣![]() x2﹣
x2﹣![]() x+c,计算即可求得c的值;
x+c,计算即可求得c的值;
(2)点D与⊙M上,理由:由(1)得抛物线的解析式为:y=﹣![]() x2﹣
x2﹣![]() x+8,进一步得到点D的坐标为(2,4),根据坐标轴上点的坐标特征可求点A的坐标为(﹣6,0),根据待定系数法可求直线AD的解析式,根据坐标轴上点的坐标特征可求点K的坐标为(0,3),在Rt△AOK中,根据三角函数得到tan∠KAO,作DE⊥y轴于点E,则DE=2,CE=8﹣4=4,在Rt△CED中,根据三角函数得到tan∠ECD,tan∠ECD=
x+8,进一步得到点D的坐标为(2,4),根据坐标轴上点的坐标特征可求点A的坐标为(﹣6,0),根据待定系数法可求直线AD的解析式,根据坐标轴上点的坐标特征可求点K的坐标为(0,3),在Rt△AOK中,根据三角函数得到tan∠KAO,作DE⊥y轴于点E,则DE=2,CE=8﹣4=4,在Rt△CED中,根据三角函数得到tan∠ECD,tan∠ECD=![]() =
=![]() ,可得∠KAO=∠ECD,进一步得到∠ECD+∠CKD=90°,∠CDK=90°,可得点D在⊙M上.
,可得∠KAO=∠ECD,进一步得到∠ECD+∠CKD=90°,∠CDK=90°,可得点D在⊙M上.
(3)分两种情况讨论:i)当直线AD在x轴的上方时;ii)当直线AD在x轴的下方时,直线AD关于x轴的对称图形为直线AD',进行讨论,可求符合条件的点D的坐标.
试题解析:(1)把C(0,8)代入抛物线y=﹣![]() x2﹣
x2﹣![]() x+c,得c=8.
x+c,得c=8.
故答案为:8;
(2)点D与⊙M上,
理由如下:由(1)得:c=8,∴抛物线的解析式为:y=﹣![]() x2﹣
x2﹣![]() x+8,
x+8,
当x=2时,y=﹣![]() ×22﹣
×22﹣![]() ×2+8=4,∴点D的坐标为(2,4),
×2+8=4,∴点D的坐标为(2,4),
在y=﹣![]() x2﹣
x2﹣![]() x+8中,令y=0,则﹣
x+8中,令y=0,则﹣![]() x2﹣
x2﹣![]() x+8=0,
x+8=0,
解得:x1=﹣6,x2=![]() ,∴点A的坐标为(﹣6,0).
,∴点A的坐标为(﹣6,0).
设直线AD的解析式为y=kx+b(k≠0),又∵直线过点A(﹣6,0)和点D(2,4),
∴![]() ,解得:
,解得:![]() ,∴直线AD的解析式为y=
,∴直线AD的解析式为y=![]() x+3.
x+3.
令x=0,则y=3,∴点K的坐标为(0,3).
在Rt△AOK中,tan∠KAO=![]() ,
,
作DE⊥y轴于点E,则DE=2,CE=8﹣4=4,
在Rt△CED中,tan∠ECD![]() ,
,
∴tan∠KAO=tan∠ECD,
即∠KAO=∠ECD
∵∠KAO+∠AKO=90°,
又∵∠AKO=∠CKD,
∴∠ECD+∠CKD=90°,∠CDK=90°,
∴点D在⊙M上.
(3)分两种情况讨论:i)当直线AD在x轴的上方时,由(2)中可知:tan∠ECD=![]() ,
,
在Rt△OED中,tan∠EOD=![]() ,∴tan∠ECD=tan∠EOD,∠ECD=∠EOD,CD=OD,
,∴tan∠ECD=tan∠EOD,∠ECD=∠EOD,CD=OD,
∵∠AOC=90°,∴点O在⊙M上.在⊙M中,![]() =
=![]() ,∠CAD=∠DAB,即∠BAC=2∠BAD,
,∠CAD=∠DAB,即∠BAC=2∠BAD,
∴点D(2,4)符合题意.
ii)当直线AD在x轴的下方时,直线AD关于x轴的对称图形为直线AD',
设直线AD'上的任意一点为(m,n),则点(m,n)关于x轴的对称点(m,﹣n)在直线AD上,
把点(m,﹣n)代入直线AD的解析式y=![]() x+3,得:﹣n=
x+3,得:﹣n=![]() m+3,n=﹣
m+3,n=﹣![]() m﹣3,即y=﹣
m﹣3,即y=﹣![]() x﹣3,
x﹣3,
联立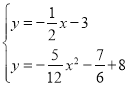 得:﹣
得:﹣![]() x﹣3=﹣
x﹣3=﹣![]() x2﹣
x2﹣![]() x+8,
x+8,
整理得:5x2+8x﹣132=0,
解得:x1=﹣6,x2=![]() ,
,
∴点D(![]() ,-
,-![]() ).
).
综上,符合条件的点D的坐标为(2,4)或(![]() ,-
,-![]() ).
).


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=mx+n的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() (x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6,
(x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6,![]() .
.
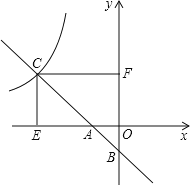
(1)求点A的坐标;
(2)求一次函数和反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凯里市万潮中学计划从天一商场购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用16元.且购买4块A型小黑板和3块B型小黑板共需680元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据万潮中学实际情况,需从天一商场购买A、B两种型号的小黑板共50块,要求购买A、B两种型号小黑板的总费用不超过4640元.并且购买A型小黑板的数量大于购买B种型号小黑板的数量的![]() .请你通过计算,求出万潮中学从天一商场购买A、B两种型号的小黑板有哪几种购买方案?
.请你通过计算,求出万潮中学从天一商场购买A、B两种型号的小黑板有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解方程3x-(x-2a)=4去括号时,忘记将括号中的第二项变号,求得方程的解为x=-2,那么方程正确的解为( )
A. x=2 B. x=4 C. x=6 D. x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列分解因式正确的是( )
A.x2﹣5x﹣6=(x+2)(x﹣3)B.x2﹣5x﹣6=(x﹣2)(x+3)
C.x2﹣5x﹣6=(x+1)(x﹣6)D.x2﹣5x﹣6=(x﹣1)(x+6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com