
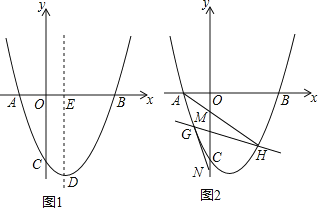
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.
(1)求该抛物线的解析式,并直接写出顶点D的坐标;
(2)如图2,直线y=![]() +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
+n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
(3)如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.
【答案】(1)y=![]() (x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4
(x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4![]() )
)
【解析】
(1)由OB=3OA可设A(-t,0),B(3t,0),代入抛物线解析式即得到关于a、t的二元方程,解方程求出a即求得抛物线解析式,配方即得到顶点D的坐标.
(2)由(1)求得t=2可知点A(-2,0),设G(x1,![]() x12-2x1-6),H(x2,
x12-2x1-6),H(x2,![]() x22-2x2-6),把直线y=
x22-2x2-6),把直线y=![]() x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
(3)以点P为圆心,PB长为半径的⊙P,由于满足PB=PQ(即点Q在⊙P上)且点Q在直线CD上的点Q有且只有一个,即⊙P与直线CD只有一个公共点,所以直线CD与⊙P相切于点Q.由(1)得点C、D坐标可知直线CD与DE夹角为45°,△PDQ为等腰直角三角形,PD=
2 |
PQ=
2 |
PB.设点P纵坐标为p,用p表示PB和PD的长并列得方程即可求p的值.由于点P在线段DE上,故p的值为负数,舍去正数解.
(1)∵抛物线y=ax2﹣4ax﹣6与x轴交于A,B两点,OB=3OA
∴设A(﹣t,0),B(3t,0)(t>0)
∴ 解得:
解得:![]()
∴抛物线解析式为y=![]() x2﹣2x﹣6=
x2﹣2x﹣6=![]() (x﹣2)2﹣8
(x﹣2)2﹣8
∴顶点D的坐标为(2,﹣8)
(2)∵t=2
∴A(﹣2,0)
设抛物线上的点G(x1,![]() x12﹣2x1﹣6),H(x2,
x12﹣2x1﹣6),H(x2,![]() x22﹣2x2﹣6)
x22﹣2x2﹣6)
∵直线y=![]() +n与抛物线交于G,H两点
+n与抛物线交于G,H两点
∴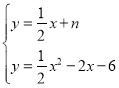 整理得:x2﹣3x﹣12﹣2n=0
整理得:x2﹣3x﹣12﹣2n=0
∴x1+x2=3
设直线AG解析式为y=kx+b,即N(0,b)(b<0)
∴
①×x1得:﹣2kx1+bx1=0 ③
②×2得:2kx1+2b=x12﹣4x1﹣12 ④
③+④得:(x1+2)b=(x1+2)(x1﹣6)
∵点G与A不重合,即x1+2≠0
∴b=x1﹣6即ON=﹣b=6﹣x1
同理可得:OM=6﹣x2
∴OM+ON=6﹣x2+6﹣x1=12﹣(x1+x2)=12﹣3=9
(3)如图,过点C作CF⊥DE于点F,以点P为圆心、PB为半径作圆

∵PB=PQ
∴点Q在⊙P上
∵有且只有一个点Q在⊙P上又在直线CD上
∴⊙P与直线CD相切于点Q
∴PQ⊥CD
由(1)得:B(6,0),C(0,﹣6),D(2,﹣8)
∴CF=2,DF=﹣6﹣(﹣8)=2,即CF=DF
∴∠CDF=45°
∴△DPQ为等腰直角三角形
∴PD=![]() PQ
PQ
∴PD2=2PQ2=2PB2
设P(2,p)(﹣8≤p≤0)
∴PD=p+8,PB2=(6﹣2)2+p2=16+p2
∴(p+8)2=16+p2
解得:p1=8﹣4![]() ,p2=8+4
,p2=8+4![]() (舍去)
(舍去)
∴点P坐标为(2,8﹣4![]() )
)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,有一格点△ABC(说明:顶点都在网格线交点处的三角形叫做格点三角形).
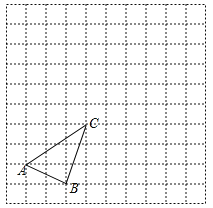
(1)将△ABC先向右平移5个单位,再向上平移2个单位,得到△A'B'C',请直接画出平移后的△A'B'C';
(2)将△A'B'C'绕点C'顺时针旋转90°,得到△A'B'C',请直接画出旋转后的△A'B'C';
(3)在(2)的旋转过程中,求点A'所经过的路线长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
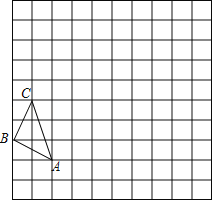
【题目】在如图的正方形网格中,每一个小正方形的边长均为1,已知格点△ABC的顶点A、C的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系.
(2)以点(﹣1,2)为位似中心,相似比为2,将△ABC放大为原来的2倍,得到△A1B1C1,画出△A1B1C1,使它与△ABC在位似中心的异侧,并写出B1点坐标为 .
(3)线段BC与线段B1C1的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、AC为圆O的弦,连接CO并延长,交AB于点D,且∠ADC=2∠C;
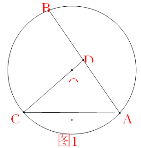
(1)如图1,求证:AD=CO;
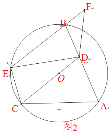
(2)如图2,取弧BC上一点E,连接EB、EC、ED,且∠EDA=∠ECA,延长EB至点F,连接FD,若∠EDF-∠F=60°,求∠BDF的度数;
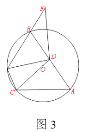
(3)如图3,在(2)的条件下,若CD=10,![]() ,求AC的长度.
,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
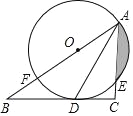
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
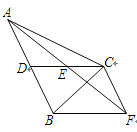
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com