
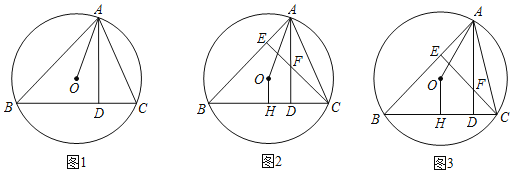
【题目】已知锐角△ABC内接于⊙O,AD⊥BC于点D,连接AO.
(1)如图1,求证:∠BAO=∠CAD;
(2)如图2,CE⊥AB于点E,交AD于点F,过点O作OH⊥BC于点H,求证:AF=2OH;
(3)如图3,在(2)的条件下,若AF=AO,tan∠BAO=![]() ,BC=
,BC=![]() ,求AC的长.
,求AC的长.
【答案】(1)详见解析;(2)详见解析;![]() +3
+3![]() .
.
【解析】
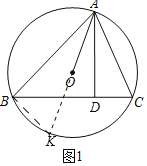
(1)延长AO交⊙O于K,连接BK.利用等角的余角相等证明即可.
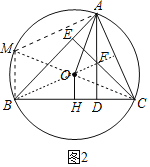
(2)延长CO交⊙O于M,连接AM,BM,连接BF.证明四边形AMBF是平行四边形,BM=2OH即可解决问题.
(3)延长CO交⊙O于M,连接AM,BM,连接BF.证明∠BAO=∠DAC=∠DBF,推出tan∠DBF=tan∠BAP=![]() =
=![]() ,设DF=x,则BD=3x,CD=2
,设DF=x,则BD=3x,CD=2![]() ﹣3x,AD=6
﹣3x,AD=6![]() ﹣9x,AF=BM=6
﹣9x,AF=BM=6![]() ﹣10x,构建方程即可解决问题.
﹣10x,构建方程即可解决问题.
(1)证明:延长AO交⊙O于K,连接BK.
∵AK是直径,
∴∠ABK=90°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠BAO+∠K=90°,∠DAC+∠C=90°,∠K=∠C,
∴∠BAO=∠DAC.
(2)证明:延长CO交⊙O于M,连接AM,BM,连接BF.
∵CM是直径,
∴∠CBM=∠MAC=90°,
∵OH⊥BC,
∴BH=CH,∠OHC=∠CBM=90°,
∴AD∥BM,
∵OC=OM,
∴BM=2OH,
∵AD⊥BC,CA⊥AB,
∴BF⊥AC,∵A⊥AC,
∴AM∥BF,
∴四边形AMBF是平行四边形,
∴AF=BM,
∴AF=2OH.
(3)解:延长CO交⊙O于M,连接AM,BM,连接BF.
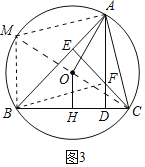
由(2)可知,四边形AMBF是平行四边形,
∴AF=BM,
∴OA=AF,
∴BM=OA,
∴CM=2BM,
∵∠CBM=90°,
∴∠BCM=30°,
∵∠BAO=∠DAC=∠DBF,
∴tan∠DBF=tan∠BAP=![]() =
=![]() ,设DF=x,则BD=3x,CD=2
,设DF=x,则BD=3x,CD=2![]() ﹣3x,AD=6
﹣3x,AD=6![]() ﹣9x,AF=BM=6
﹣9x,AF=BM=6![]() ﹣10x,
﹣10x,
∵BC=2![]() ,
,
∴BM=BCtan30°=2![]() ,
,
∴6![]() ﹣10x=2
﹣10x=2![]() ,
,
∴x=![]() ,
,
∴AC=![]() =
=![]() +3
+3![]() .
.


科目:初中数学 来源: 题型:
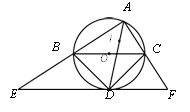
【题目】如图,A是以BC为直径的⊙O上一点,I是△ABC的内心,AI的延长线交⊙O于点D,过点D作BC的平行线交AB、AC的延长线于E、F.下列说法:①△DBC是等腰直角三角形;②EF与⊙O相切;③EF=2BC;④点B、I、C在以点D 为圆心的同一个圆上.其中一定正确的是_______(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+1)x+m2﹣4=0有两个不相等的实数根
(1)求实数m的取值范围;
(2)若两个实数根的平方和等于15,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
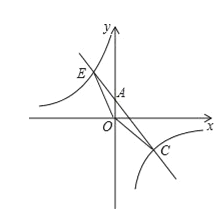
【题目】如图,反比例函数y=![]() 的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
(1)求反比例函数与一次函数的解析式;
(2)求△COE的面积;
(3)点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
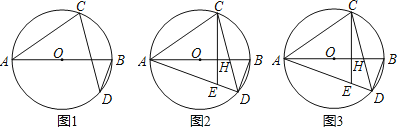
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)若∠ABD=α,求∠BDC(用α表示);
(2)过点C作CE⊥AB于H,交AD于E,∠CAD=β,求∠ACE(用β表示);
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com