
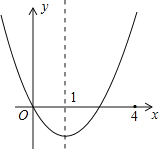
【题目】二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣2t=0(t为实数)在﹣1<x≤4的范围内有解,则t的取值范围是_____.
【答案】﹣0.5≤t≤4
【解析】
一元二次方程x2+bx﹣2t=0(t为实数)在﹣1<x≤4的范围内有解,即直线y=2t与二次函数y=x2+bx,在这个范围内有交点,则:y=2t在顶点和x=4时之间时,两个函数有交点,即可求解.
解:∵抛物线的对称轴为直线x=﹣![]() =1,解得b=﹣2,
=1,解得b=﹣2,
∴抛物线解析式为y=x2﹣2x,顶点坐标为(1,﹣1),
当x=﹣1时,y=3,当x=4时,y=8,
∵一元二次方程x2+bx﹣2t=0(t为实数)在﹣1<x≤4的范围内有解,
∴直线y=2t与二次函数y=x2+bx在﹣1<x≤4范围内有交点,
∴﹣1≤2t≤8,
∴﹣0.5≤t≤4.
故答案为:﹣0.5≤t≤4.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
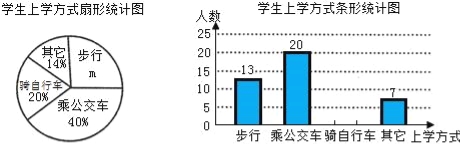
(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 网络比
网络比![]() 网络的传输速度快10倍以上,因此人们对
网络的传输速度快10倍以上,因此人们对![]() 产品充满期待.华为集团计划2020年元月开始销售一款
产品充满期待.华为集团计划2020年元月开始销售一款![]() 产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第
产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第![]() 个月(
个月(![]() 为正整数)销售价格为
为正整数)销售价格为![]() 元/台,
元/台,![]() 与
与![]() 满足如图所示的一次函数关系:且第
满足如图所示的一次函数关系:且第![]() 个月的销售数量
个月的销售数量![]() (万台)与
(万台)与![]() 的关系为
的关系为![]() .
.
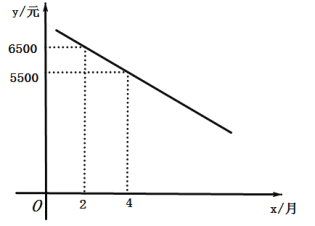
(1)该产品第6个月每台销售价格为______元;
(2)求该产品第几个月的销售额最大?该月的销售价格是多少元/台?
(3)若华为董事会要求销售该产品的月销售额不低于27500万元,则预计销售部符合销售要求的是哪几个月?
(4)若每销售1万台该产品需要在销售额中扣除![]() 元推广费用,当
元推广费用,当![]() 时销售利润最大值为22500万元时,求
时销售利润最大值为22500万元时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系x0y中,对于图形G,若存在一个正方形γ,这个正方形的某条边与x轴垂直,且图形G上的所有的点都在该正方形的内部或者边上,则称该正方形γ为图形G的一个正覆盖.很显然,如果图形G存在一个正覆盖,则它的正覆盖有无数个,我们将图形G的所有正覆盖中边长最小的一个,称为它的紧覆盖.如图所示,图形G为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形G的正覆盖,其中正方形ABCD就是图形G的紧覆盖.

(1)对于半径为2的⊙0,它的紧覆盖的边长为 .
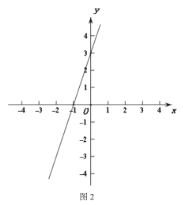
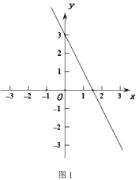
(2)如图1,点P为直线y=-2x+3上一动点,若线段OP的紧覆盖的边长为2,求点P的坐标;
(3)如图2,直线y=3x+3与x轴,y轴分别交于A,B,
①以0为圆心,r为半径的⊙0与线段AB有公共点,且由⊙0与线段AB组成的图形G的紧覆盖的边长小于4,直接写出r的取值范围;
②若在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆盖的边长为3,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
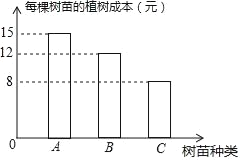
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△FHG中,![]() H=90°,FH∥x轴,
H=90°,FH∥x轴,![]() ,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数
,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数![]() 的图像与x轴交于A、B两点,与y轴交于点E(0,
的图像与x轴交于A、B两点,与y轴交于点E(0,![]() ),顶点为C(1,
),顶点为C(1,![]() ),点D为二次函数
),点D为二次函数![]() 图像的顶点.
图像的顶点.
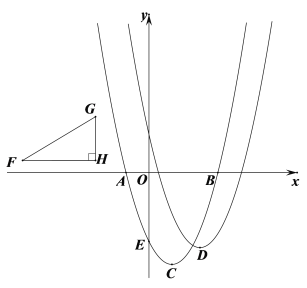
(1)求二次函数y1的函数关系式;
(2)若准黄金直角三角形的顶点F与点A重合、G落在二次函数y1的图像上,求点G的坐标及△FHG的面积;
(3)设一次函数y=mx+m与函数y1、y2的图像对称轴右侧曲线分别交于点P、Q. 且P、Q两点分别与准黄金直角三角形的顶点F、G重合,求m的值并判断以C、D、Q、P为顶点的四边形形状,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
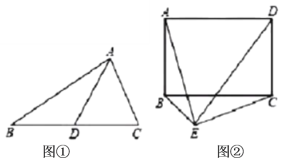
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接与⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF。
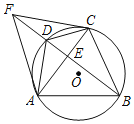
(1)若∠CAD=α,求∠BAC(用含α的代数式表示);
(2)求证:CF是⊙O的切线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com