
【题目】如图,四边形ABCD内接与⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF。
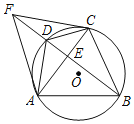
(1)若∠CAD=α,求∠BAC(用含α的代数式表示);
(2)求证:CF是⊙O的切线。
【答案】(1)∠BAC=2α;(2)见解析
【解析】
(1)根据等腰三角形的性质得出∠ABC=∠ACB,根据圆心角、弧、弦的关系得到![]() ,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=
,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=![]() (180°-∠BAC)=90°-
(180°-∠BAC)=90°-![]() ∠BAC,∠ADB=90°-∠CAD,从而得到
∠BAC,∠ADB=90°-∠CAD,从而得到![]() ∠BAC=∠CAD,即可证得结论;
∠BAC=∠CAD,即可证得结论;
(2)连接OA,OC,设∠CAD=α,∠ABD=β,则可得∠AOC=2(α+β),从而可求出∠ACO=90°-α-β,由圆周角定理可得∠BDC=2α,因为DF=DC,所以∠DCF=∠DFC=α,可求得∠DCF+∠DCA+∠DCO=90°,从而可得结论.
(1)∵AB=AC,
∴![]() ,∠ABC=∠ACB,
,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=![]() (180°-∠BAC)=90°-
(180°-∠BAC)=90°-![]() ∠BAC,
∠BAC,
∵BD⊥AC,
∴∠ADB=90°-∠CAD,
∴![]() ∠BAC=∠CAD,
∠BAC=∠CAD,
∴∠BAC=2∠CAD;
∵∠CAD=α,
∴∠BAC=2α;
(2)连接OA,OC,设∠CAD=α,∠ABD=β,
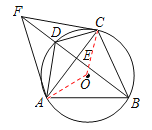
∴∠ABC=α+β,∠ACD=β
∴∠AOC=2(α+β),
∵AO=OC
∴∠ACO=![]() ,
,
由(1)得∠BAC=2α,
∴∠BDC=2α
∵DF=DC
∴∠DFC=∠DCF,
∴∠DFC+∠DCF=2α,即∠DCF=α,
∵∠OCF=∠OCA+∠ACD+∠DCF=90°-α-β+β+α=90°,
∴OC⊥FC,
∴CF是⊙O的切线.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
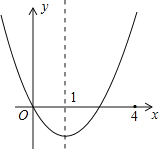
【题目】二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣2t=0(t为实数)在﹣1<x≤4的范围内有解,则t的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有2000名学生参加了2018年全省八年级数学学业水平测试.其中有这样一题:如图,分别以线段BD的端点B、D为圆心,相同的长为半径画弧,两弧相交于A、C两点,连接AB、AD、CB、CD.若AB=2,BD=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.

统计我市学生解答和得分情况,并制作如下图表:

(1)求学业水平测试中四边形ABCD的面积;
(2)请你补全条形统计图;
(3)我市该题的平均得分为多少?
(4)我市得3分以上的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:![]() ,验证:
,验证:![]() ,验证:
,验证:![]() .
.
(1)按照上述两个等式及其验证过程,猜想![]() 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,直接写出用a(a≥2的整数)表示的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 和等腰直角
和等腰直角![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
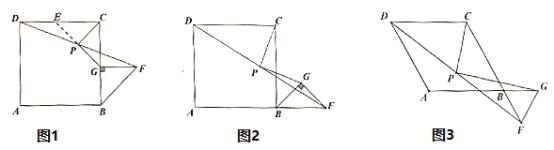
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上时,(1)中的结论是否成立?请证明你的结论;
的延长线上时,(1)中的结论是否成立?请证明你的结论;
(3)如图3,若四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 、
、![]() 又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()

(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
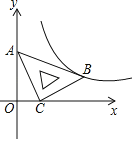
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(![]() ,0)B.(2,0)C.(
,0)B.(2,0)C.(![]() ,0)D.(3,0)
,0)D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
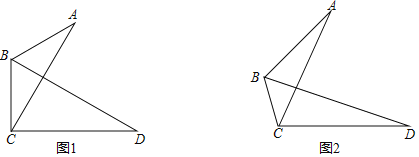
【题目】在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.
(1)如图1,若AB=BC,求证:BD平分∠ABC;
(2)如图2,若AB=2BC,
①求![]() 的值;
的值;
②连接AD,当S△ABC=![]() 时,直接写出四边形ABCD的面积为 .
时,直接写出四边形ABCD的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com