
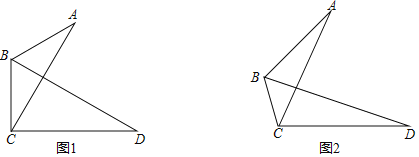
【题目】在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.
(1)如图1,若AB=BC,求证:BD平分∠ABC;
(2)如图2,若AB=2BC,
①求![]() 的值;
的值;
②连接AD,当S△ABC=![]() 时,直接写出四边形ABCD的面积为 .
时,直接写出四边形ABCD的面积为 .
【答案】(1)详见解析;(2)① ![]() ;②
;② ![]() .
.
【解析】
(1)连接AD,证△ACD是等边三角形,再证△ABD≌△CBD,推出∠CBD=∠ABD,即得出结论;
(2)①连接AD,作等边三角形ACD的外接圆⊙O,证点B在⊙O上,在BD上截取BM,使BM=BC,证△CBA≌△CMD,设BC=BM=1,则AB=MD=2,BD=3,过点C作CN⊥BD于N,可求出BN=![]() BC=
BC=![]() ,CN=
,CN=![]() BC=
BC=![]() ,ND=BD﹣BN=
,ND=BD﹣BN=![]() ,CD=
,CD=![]() ,即可求出
,即可求出![]() =
=![]() =
=![]() ;
;
②分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=![]() ,AH=
,AH=![]() ﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ的值,求出
﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ的值,求出![]() =
=![]() ,因为AC为△ABC与△ACD的公共底,所以
,因为AC为△ABC与△ACD的公共底,所以![]() =
=![]() ,可求出△ACD的面积,进一步求出四边形ABCD的面积.
,可求出△ACD的面积,进一步求出四边形ABCD的面积.
(1)证明:如图1,连接AD,
由题意知,∠ACD=60°,CA=CD,
∴△ACD是等边三角形,
∴CD=AD,
又∵AB=CB,BD=BD,
∴△ABD≌△CBD(SSS),
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)解:①如图2,连接AD,作等边三角形ACD的外接圆⊙O,
∵∠ADC=60°,∠ABC=120°,
∴∠ADC+∠ABC=180°,
∴点B在⊙O上,
∵AD=CD,
∴![]() ,
,
∴∠CBD=∠CAD=60°,
在BD上截取BM,使BM=BC,
则△BCM为等边三角形,
∴∠CMB=60°,
∴∠CMD=120°=∠CBA,
又∵CB=CM,∠BAC=∠BDC,
∴△CBA≌△CMD(AAS),
∴MD=AB,
设BC=BM=1,则AB=MD=2,
∴BD=3,
过点C作CN⊥BD于N,
在Rt△BCN中,∠CBN=60°,
∴∠BCN=30°,
∴BN=![]() BC=
BC=![]() ,CN=
,CN=![]() BC=
BC=![]() ,
,
∴ND=BD﹣BN=![]() ,
,
在Rt△CND中,
CD=![]() =
=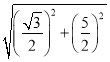 =
=![]() ,
,
∴AC=![]() ,
,
∴![]() =
=![]() ;
;
②如图3,分别过点B,D作AC的垂线,垂足分别为H,Q,
设CB=1,AB=2,CH=x,
则由①知,AC=![]() ,AH=
,AH=![]() -x,
-x,
在Rt△BCH与Rt△BAH中,
BC2﹣CH2=AB2﹣AH2,
即1﹣x2=22-(![]() -x)2,
-x)2,
解得,x=![]() ,
,
∴BH=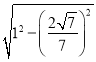 =
=![]() ,
,
在Rt△ADQ中,DQ=![]() AD=
AD=![]() ×
×![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵AC为△ABC与△ACD的公共底,
∴![]() =
=![]() =
=![]() ,
,
∵S△ABC=![]() ,
,
∴S△ACD=![]() ,
,
∴S四边形ABCD=![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
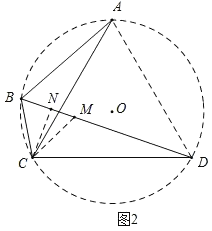
【题目】如图,四边形ABCD内接与⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF。
(1)若∠CAD=α,求∠BAC(用含α的代数式表示);
(2)求证:CF是⊙O的切线。
查看答案和解析>>
科目:初中数学 来源: 题型:
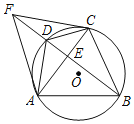
【题目】如图,点![]() 是
是![]() 中
中![]() 边的中点,
边的中点,![]() 于
于![]() ,以
,以![]() 为直径的
为直径的![]() 经过
经过![]() ,连接
,连接![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是
是![]() 的切线.其中正确的结论是( )
的切线.其中正确的结论是( )
A.①②B.①②③C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .平行四边形
.平行四边形![]() 的顶点
的顶点![]() 在线段
在线段![]() 上(点
上(点![]() 在
在![]() 的左边),顶点
的左边),顶点![]() 分别在线段
分别在线段![]() 和
和![]() 上.
上.
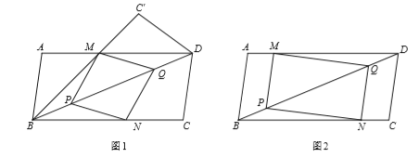
(1)求证:![]() ;
;
(2)如图1,将![]() 沿直线
沿直线![]() 折叠得到
折叠得到![]() ,当
,当![]() 恰好经过点
恰好经过点![]() 时,求证:四边形
时,求证:四边形![]() 是菱形;
是菱形;
(3)如图2,若四边形![]() 是矩形,且
是矩形,且![]() ,求
,求![]() 的长.(结果中的分母可保留根式)
的长.(结果中的分母可保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为吸引市民组团去风景区旅游,观光旅行社推出了如下收费标准:

某单位员工去风景区旅游,共支付给旅行社旅游费用10500元,请问该单位这次共有多少员工去风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东53°方向,距离B地516千米,C地位于A地南偏东45°方向.现打算打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(结果精确到1千米)(参考数据:sin53°=![]() ,cos53°=
,cos53°=![]() ,tan53°=
,tan53°=![]() )
)
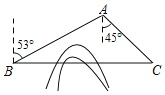
查看答案和解析>>
科目:初中数学 来源: 题型:
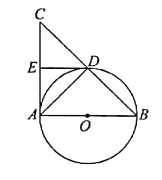
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com