
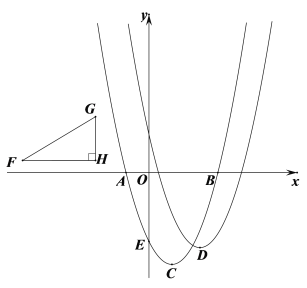
【题目】如图,Rt△FHG中,![]() H=90°,FH∥x轴,
H=90°,FH∥x轴,![]() ,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数
,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数![]() 的图像与x轴交于A、B两点,与y轴交于点E(0,
的图像与x轴交于A、B两点,与y轴交于点E(0,![]() ),顶点为C(1,
),顶点为C(1,![]() ),点D为二次函数
),点D为二次函数![]() 图像的顶点.
图像的顶点.
(1)求二次函数y1的函数关系式;
(2)若准黄金直角三角形的顶点F与点A重合、G落在二次函数y1的图像上,求点G的坐标及△FHG的面积;
(3)设一次函数y=mx+m与函数y1、y2的图像对称轴右侧曲线分别交于点P、Q. 且P、Q两点分别与准黄金直角三角形的顶点F、G重合,求m的值并判断以C、D、Q、P为顶点的四边形形状,请说明理由.
【答案】(1)y=(x-1)2-4;(2)点G坐标为(3.6,2.76),S△FHG=6.348;(3)m=0.6,四边形CDPQ为平行四边形,理由见解析.
【解析】
(1)利用顶点式求解即可,(2)将G点代入函数解析式求出坐标,利用坐标的特点即可求出面积,(3)作出图象,延长QH,交x轴于点R,由平行线的性质得证明△AQR∽△PHQ,设Q[n,0.6(n+1)],代入y=mx+m中,即可证明四边形CDPQ为平行四边形.
(1)设二次函数的解析式是y=a(x-h)2+k,(a≠0),由题可知该抛物线与y轴交于点E(0,![]() ),顶点为C(1,
),顶点为C(1,![]() ),
),
∴y=a(x-1)2-4,代入E(0,![]() ),解得a=1,
),解得a=1,
![]() (
(![]() )
)
(2)设G[a,0.6(a+1)],代入函数关系式,
得,![]() ,
,
解得a1=3.6,a2=-1(舍去),
所以点G坐标为(3.6,2.76).
S△FHG=6.348
(3)y=mx+m=m(x+1),
当x=-1时,y=0,
所以直线y=mx+m
延长QH,交x轴于点R,
由平行线的性质得,QR⊥x轴.
因为FH∥x轴,
所以∠QPH=∠QAR,
因为∠PHQ=∠ARQ=90°,
所以△AQR∽△PQH,
所以![]() =0.6,
=0.6,
设Q[n,0.6(n+1)],代入y=mx+m中,
mn+m=0.6(n+1),m(n+1)=0.6(n+1),
因为n+1≠0,
所以m=0.6..
因为y2=(x-1-m)2+0.6m-4,
所以点D由点C向右平移m个单位,再向上平移0.6m个单位所得,
过D作y轴的平行线,交x轴与K,再作CT⊥KD,交KD延长线与T,
所以![]() =0.6,
=0.6,
所以tan∠KSD=tan∠QAR,
所以∠KSD=∠QAR,
所以AQ∥CS,即CD∥PQ.
因为AQ∥CS,由抛物线平移的性质可得,CT=PH,DT=QH,
所以PQ=CD,
所以四边形CDPQ为平行四边形.



科目:初中数学 来源: 题型:
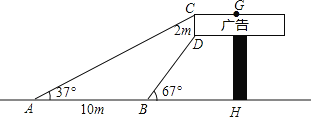
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
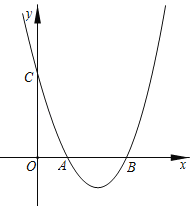
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点 C.
(1)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(2)在(1)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
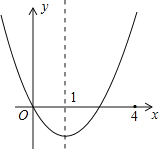
【题目】二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣2t=0(t为实数)在﹣1<x≤4的范围内有解,则t的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
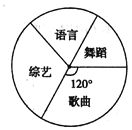
【题目】郑州市长跑协会为庆祝协会成立十周年,计划在元且期间进行文艺会演,陈老师按拟报项目歌曲舞蹈、语言、综艺进行统计,将统计结果绘成如图所示的两幅不完整的统计图.
(1)请补全条形统计图;
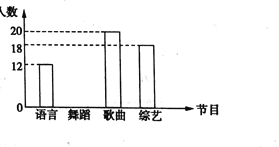
(2)语言类所占百分比为______,综艺类所在扇形的圆心角度数为______;
(3)在前期彩排中,经过各位评委认真审核,最终各项目均有一队员得分最高,若从这四名队员(两男两女)中选择两人发表感言,求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
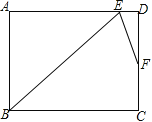
【题目】如图,在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=8,DF=3FC,则BC=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
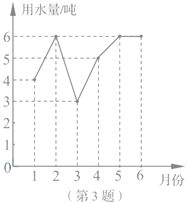
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有2000名学生参加了2018年全省八年级数学学业水平测试.其中有这样一题:如图,分别以线段BD的端点B、D为圆心,相同的长为半径画弧,两弧相交于A、C两点,连接AB、AD、CB、CD.若AB=2,BD=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.

统计我市学生解答和得分情况,并制作如下图表:

(1)求学业水平测试中四边形ABCD的面积;
(2)请你补全条形统计图;
(3)我市该题的平均得分为多少?
(4)我市得3分以上的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()

(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com