
【题目】某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;
(2)补全条形统计图,并计算阅读部分圆心角是 度.
(3)若该校九年级爱好阅读的学生有150人,估计九年级有 名学生?
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为对角线AC(不含点A)上任意一点,AB=![]() ;
;
(1)如图1,将△ADE绕点D逆时针旋转90°得到△DCF,连接EF;
①把图形补充完整(无需写画法); ②求![]() 的取值范围;
的取值范围;
(2)如图2,求BE+AE+DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
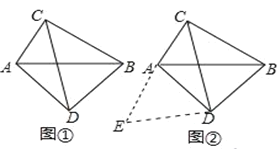
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
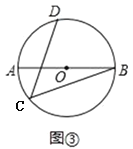
简单应用:
(1)在图①中,若AC=2,BC=4,则CD= .
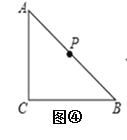
(2)如图③,AB是⊙O的直径,点C、D在⊙上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图4,△ABC中,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,琼海市在国际和国内的知名度越来越大,带动旅游事业蓬勃发展,吸引大批海内外游客前来观光旅游、购物度假,下面的图1和2分别反映了该市2011-2014年游客总人数和旅游业总收入情况.根据统计图提供的信息,解答下列问题:
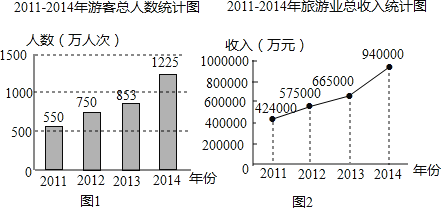
(1)2014年游客总人数为 万人次,旅游业总收入为 万元;
(2)在2012年,2013年,2014年这三年中,旅游业总收入增长幅度最大的是 年,这一年的旅游业总收入比上一年增长的百分率为 (精确到1%);
(3)据统计,2014年琼海共接待国内游客1200万人,人均消费约700元.求海外游客人均消费约多少元?(注:旅游收入=游客人数×游客的人均消费)
查看答案和解析>>
科目:初中数学 来源: 题型:
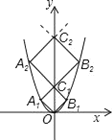
【题目】如图,已知点A1,A2,…,A2019在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2019在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2018A2019C2019B2019都是正方形,则正方形C2018A2019C2019B2019的边长_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,![]() .线段
.线段![]() 与线段
与线段![]() 存在一种变换关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标为__________.
存在一种变换关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com