
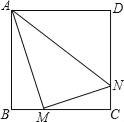
【题目】如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A.8B.4![]()
![]() C.10D.8
C.10D.8![]()
【答案】C
【解析】
通过正方形的性质可以证明Rt△ABM∽Rt△MCN,设BM=x,可得CN=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣4)2+2,根据二次函数的性质,可得CN的最大值,再根据勾股定理即可求出AN的长度.
(x﹣4)2+2,根据二次函数的性质,可得CN的最大值,再根据勾股定理即可求出AN的长度.
解:在正方形ABCD中,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠BAM+∠AMB=90°,
∴∠BAM=∠CMN,
∴Rt△ABM∽Rt△MCN;
设BM=x,
∴![]() ,即
,即![]()
整理得:CN=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣4)2+2,
(x﹣4)2+2,
∴当x=4时,CN取得最大值2,
∵![]()
∴当DN取得最小值、CN取得最大值,即DN=6时,AN最小,
则AN=![]() =10,
=10,
故选:C.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=4![]() ,把边CD绕点C逆时针旋转30度得到线段CE,连接BE并延长,交AD于点F,连接DE,则线段EF的长度为________
,把边CD绕点C逆时针旋转30度得到线段CE,连接BE并延长,交AD于点F,连接DE,则线段EF的长度为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请用配方法探索有实数根的条件,并推导出求根公式,证明x1x2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 与原点重合点
与原点重合点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.
轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;
(2)补全条形统计图,并计算阅读部分圆心角是 度.
(3)若该校九年级爱好阅读的学生有150人,估计九年级有 名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线y=![]() (x>0)交于点A(1,a).
(x>0)交于点A(1,a).
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n)(m>3)是直线l上一动点,过点P分别作x轴、y轴的平行线,交双曲线y=![]() (x>0)于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W.横、纵坐标都是整数的点叫做整点.
(x>0)于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W.横、纵坐标都是整数的点叫做整点.
①当m3 时,直接写出区域W 内的整点个数;
②若区域W 内有整点,且个数不超过 5 个,结合图象,求 m 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com