
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+k��˫����y��![]() ��x��0�����ڵ�A��1��a����
��x��0�����ڵ�A��1��a����
��1����a��k��ֵ��
��2����ֱ֪��l����D��2��0����ƽ����ֱ��y��kx+k����P��m��n����m��3����ֱ��l��һ���㣬����P�ֱ���x�ᡢy���ƽ���ߣ���˫����y��![]() ��x��0���ڵ�M��N��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��ΪW���ᡢ�����궼�������ĵ�������㣮
��x��0���ڵ�M��N��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��ΪW���ᡢ�����궼�������ĵ�������㣮
�ٵ�m3 ʱ��ֱ��д������W �ڵ����������
��������W �������㣬�Ҹ��������� 5 �������ͼ���� m ��ȡֵ��Χ��
���𰸡���1��![]() ����2��0����3��
����2��0����3��![]() ��
��![]() ��
��
��������
��1������A��1��a�������������Ľ���ɵô𰸣�
��2������ƽ��![]() �ҹ�D��ֱ�߽���ʽ���������⻭��ͼ�Σ��۲��������ɵõ��٢ڵĴ𰸣�
�ҹ�D��ֱ�߽���ʽ���������⻭��ͼ�Σ��۲��������ɵõ��٢ڵĴ𰸣�
�⣺��1����A��1��a������![]() ��
��![]() ��
��
����A��1��4��������![]() ������
������![]() ����ã�
����ã�![]() ��
��
��2���١�ֱ��l����D��2��0����ƽ����ֱ��y=2x+2��
��ֱ��![]() �Ľ���ʽΪy=2x-4��
�Ľ���ʽΪy=2x-4��
��![]() ʱ��
ʱ��![]() ��
��
���P��������3��2����
�������⻭��ͼ������ͼ��ʾ��
�۲�ͼ�Σ���֪������W�ڵ����������0��
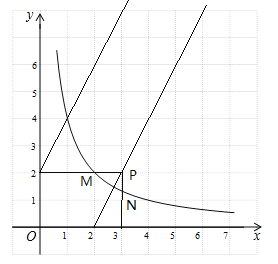
������ͼ��������W �������㣬�Ҹ���������5�������ͼ��ã�P���߶�QH�ϣ��Ҳ���H�غϣ���ͼ��֪��Q��4��4����
��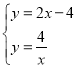 ��ã�
��ã�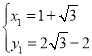 ��
��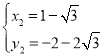
���ԣ�H![]()
���ԣ�![]() ��
��![]()
![]()
![]()


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
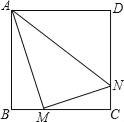
����Ŀ����ͼ��������ABCD�߳�Ϊ8��M��N�ֱ��DZ�BC��CD�ϵ��������㣬��AM��MN����AN����Сֵ�ǣ�������
A.8B.4![]()
![]() C.10D.8
C.10D.8![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ڹ��ʺ��ڵ�֪����Խ��Խ����������ҵ���չ�����������������ο�ǰ���۹����Ρ�����ȼ٣������ͼ1��2�ֱ�ӳ�˸���2011-2014���ο�������������ҵ���������������ͳ��ͼ�ṩ����Ϣ������������⣺
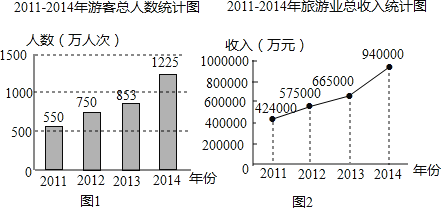
��1��2014���ο�������Ϊ ���˴Σ�����ҵ������Ϊ ��Ԫ��
��2����2012�꣬2013�꣬2014���������У�����ҵ�������������������� �꣬��һ�������ҵ���������һ�������İٷ���Ϊ ����ȷ��1%����
��3����ͳ�ƣ�2014���������Ӵ������ο�1200���ˣ��˾�����Լ700Ԫ�������ο��˾�����Լ����Ԫ����ע����������=�ο��������ο͵��˾����ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
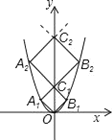
����Ŀ����ͼ����֪��A1��A2������A2019�ں���y=x2λ�ڵڶ�����ͼ���ϣ���B1��B2������B2011�ں���y=x2λ�ڵ�һ����ͼ���ϣ���C1��C2������C2019��y����������ϣ����ı���OA1C1B1��C1A2C2B2������C2018A2019C2019B2019���������Σ���������C2018A2019C2019B2019�ı߳�_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
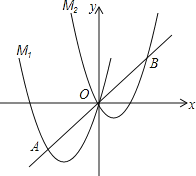
����Ŀ����ͼ����������M1��y��ax2+4x����ƽ��3����λ��������ƽ��3����λ���õ�������M2��ֱ��y��x��M1��һ�������ΪA����M2��һ�������ΪB����A�ĺ������ǩ�3��
��1����a��ֵ��M2�ı���ʽ��
��2����C���߶�AB�ϵ�һ�����㣬����C��x��Ĵ��ߣ�����ΪD����CD���Ҳ���������CDEF��
������C�ĺ�����Ϊ2ʱ��ֱ��y��x+nǡ�þ���������CDEF�Ķ���F�����ʱn��ֵ��
���ڵ�C���˶������У���ֱ��y��x+n��������CDEFʼ��û�й����㣬��n��ȡֵ��Χ��ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
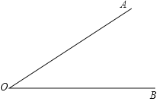
����Ŀ��������С����Ƶ�����һ���ǵ�����֪�ǵ�2�����ij߹���ͼ���̣�
��֪��![]() ��
��
������![]() ��ʹ��
��ʹ��![]() ��
��
��������ͼ��
��������![]() ����ȡһ��
����ȡһ��![]() ��
��
�����߶�![]() �Ĵ�ֱƽ���ߣ���
�Ĵ�ֱƽ���ߣ���![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
������![]() ��
��
����![]() ��Ϊ�������Ľǣ�
��Ϊ�������Ľǣ�
����С����Ƶij߹���ͼ���̣�
(1)ʹ��ֱ�ߺ�Բ�油ȫͼ��(������ͼ�ۼ�)��
(2)��������֤��(˵������������д����������)��
֤������![]() ���߶�
���߶�![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ______(______)
______(______)
��![]() ��
��
��![]() (______)
(______)
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������¹涨������ͼ��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() Ϊ
Ϊ![]() ����һ�㣬����߶�
����һ�㣬����߶�![]() �ij��ȴ�����Сֵ���ͳƸ���СֵΪ����ͼ��
�ij��ȴ�����Сֵ���ͳƸ���СֵΪ����ͼ��![]() ��
��![]() ֮��ľ��룮
֮��ľ��룮
��ƽ��ֱ������ϵxOy�У�0Ϊ����ԭ�㣮
��1����![]() ������Ϊ
������Ϊ![]() �����
�����![]() ������
������![]() ֮��ľ���Ϊ______����
֮��ľ���Ϊ______����![]() ������
������![]() ֮��ľ���Ϊ����������
֮��ľ���Ϊ����������
��2�����ֱ��![]() ��˫����
��˫����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����ô
����ô![]() ____��(����ͼ1�н����о�)
____��(����ͼ1�н����о�)
��3����![]() ������Ϊ
������Ϊ![]() ��������
��������![]() ��ԭ��
��ԭ��![]() ��ʱ����ת
��ʱ����ת![]() ���õ�����
���õ�����![]() ��������ƽ�������к�����
��������ƽ�������к�����![]() ֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��
֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��![]() ��
��
������ͼ2�л���ͼ��![]() ��������ͼ��
��������ͼ��![]() ����ɲ��֣�(���漰ƽ����ij������ʱ��������Ӱ��ʾ)
����ɲ��֣�(���漰ƽ����ij������ʱ��������Ӱ��ʾ)
�ڽ�����![]() ��ɵ�ͼ�μ�Ϊͼ��
��ɵ�ͼ�μ�Ϊͼ��![]() ��������
��������![]() ��ͼ��
��ͼ��![]() �Ĺ������ּ�Ϊͼ��
�Ĺ������ּ�Ϊͼ��![]() ����ֱ��д��ͼ��
����ֱ��д��ͼ��![]() ��ͼ��
��ͼ��![]() ֮��ľ��룮
֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1�������������У�![]() ���߶�
���߶�![]() ���߶�
���߶�![]() ����һ�ֱ任��ϵ��������һ���߶�����ij����תһ���Ƕȿ��Եõ���һ���߶Σ��������ת���ĵ�����Ϊ__________��
����һ�ֱ任��ϵ��������һ���߶�����ij����תһ���Ƕȿ��Եõ���һ���߶Σ��������ת���ĵ�����Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����5x+5��x�ᡢy��ֱ���A��C���㣬������y��x2+bx+c����A��C���㣬��x�ύ����һ��B��
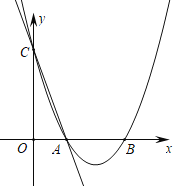
��1���������߽���ʽ��B�����ꣻ
��2��x2+bx+c����5x+5�Ľ⼯�� ����
��3������M�ڵ�һ��������������һ���㣬����MA��MB������M�˶���ijһλ��ʱ����ABM���Ϊ��ABC�������![]() �������ʱ��M�����꣮
�������ʱ��M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com