
����Ŀ��������С����Ƶ�����һ���ǵ�����֪�ǵ�2�����ij߹���ͼ���̣�
��֪��![]() ��
��
������![]() ��ʹ��
��ʹ��![]() ��
��
��������ͼ��
��������![]() ����ȡһ��
����ȡһ��![]() ��
��
�����߶�![]() �Ĵ�ֱƽ���ߣ���
�Ĵ�ֱƽ���ߣ���![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
������![]() ��
��
����![]() ��Ϊ�������Ľǣ�
��Ϊ�������Ľǣ�
����С����Ƶij߹���ͼ���̣�
(1)ʹ��ֱ�ߺ�Բ�油ȫͼ��(������ͼ�ۼ�)��
(2)��������֤��(˵������������д����������)��
֤������![]() ���߶�
���߶�![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ______(______)
______(______)
��![]() ��
��
��![]() (______)
(______)
��![]() ��
��
���𰸡�(1)��������(2)�߶δ�ֱƽ����������һ�㣬���߶����˵�ľ�����ȣ�����������һ����ǵ������������ڵ����ڽǵĺͣ�
��������
(1)���ݼ������Ի�����Ӧ�ļ���ͼ�Σ�
(2)�ȸ����߶δ�ֱƽ���ߵ����ʵõ�![]() ������ݵ��������ε����ʵõ�
������ݵ��������ε����ʵõ�![]() ��Ȼ�����������������ʵõ�
��Ȼ�����������������ʵõ�![]() ��
��
(1)��ͼ��![]() ��Ϊ��������
����������
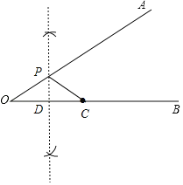
(2)֤������![]() ���߶�
���߶�![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() (�߶δ�ֱƽ����������һ�㣬���߶����˵�ľ������)
(�߶δ�ֱƽ����������һ�㣬���߶����˵�ľ������)
��![]() ��
��
��![]() (����������һ����ǵ������������ڵ����ڽǵĺ�)
(����������һ����ǵ������������ڵ����ڽǵĺ�)
��![]() ��
��
�ʴ�Ϊ���߶δ�ֱƽ����������һ�㣬���߶����˵�ľ�����ȣ�����������һ����ǵ������������ڵ����ڽǵĺͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
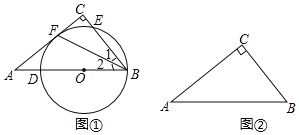
����Ŀ����Rt��ABC�У���C��90����
��1����ͼ�٣���O��б��AB�ϣ��Ե�OΪԲ�ģ�OB��Ϊ�뾶��Բ��AB�ڵ�D����BC�ڵ�E�����AC�����ڵ�F����֤����1����2��
��2����ͼ��������M��ʹ������������������Բ���ڱ�AB�ϣ��ھ�����B�������AC���У����߹���ͼ��ֻ������ͼ�ۼ�����Ҫ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���BAD��60����AC��BD���ڵ�O��EΪCD�ӳ����ϵ�һ�㣬��CD��DE������BE�ֱ�AC��AD�ڵ�F��G������OG�������н��ۣ���OG��![]() AB��������EGDȫ�ȵ������ι���5������S�ı���ODGF��S��ABF�����ɵ�A��B��D��E���ɵ��ı��������Σ�������ȷ���ǣ�������
AB��������EGDȫ�ȵ������ι���5������S�ı���ODGF��S��ABF�����ɵ�A��B��D��E���ɵ��ı��������Σ�������ȷ���ǣ�������
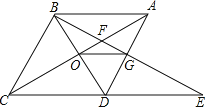
A.�٢�B.�٢ۢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=x+4��ͼ���뷴��������y=![]() ��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��1����˷����������ı���ʽ��
��2������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������400Ԫ����������ֻ���ã�������440ԪҲ��������ֻͬ�������ã������۱����Ź�������õĵ��۹�5Ԫ��
��1�����������������ù��ж���ֻ��
��2��һ�������������������������������2ֻ��������������������������2����1ֻ�����˽�����ȫ���۳������ۼ�����Ϊ����Ԫʱ����������õ���������960Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
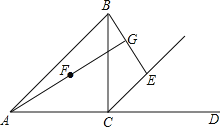
����Ŀ����ͼ����ABC�У���ACB��90����AC��BC��EΪ��ǡ�BCDƽ������һ���㣨�����C�غϣ�����E����ֱ��BC�ĶԳƵ�ΪF������BE������AF���ӳ���ֱ��BE�ڵ�G��
��1����֤��AF��BE��
��2���õ�ʽ��ʾ�߶�FG��EG��CE��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
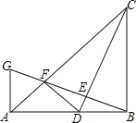
����Ŀ����ͼ����Rt��ABC�У���ABC=90����AB=BC����D���߶�AB�ϵ�һ�㣬����CD������B��BG��CD���ֱ�CD��CA�ڵ�E��F�������A�Ҵ�ֱ��AB��ֱ���ཻ�ڵ�G������DF�����������ĸ����ۣ���![]() ��������D��AB���е㣬��AF��
��������D��AB���е㣬��AF��![]() AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������
AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������![]() ����S��ABC��9S��BDF��������ȷ�Ľ��������______��
����S��ABC��9S��BDF��������ȷ�Ľ��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��3x+3��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵ�һ������������ABCD����D��˫����![]() ��k��0���ϣ�����������x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ�����ڸ�˫�����ϣ���a��ֵ��
��k��0���ϣ�����������x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ�����ڸ�˫�����ϣ���a��ֵ��

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ��������ĸ����������Ĵ�������Ϸ����Ϸ�����ǣ���һ���ɼ�����������ҡ������������е�ijһ���е�ijһ�ˣ��Ժ��ÿһ�δ��������ɽӵ�����������������������е�ijһ�ˣ�
��1����һ�δ���ʱ��ǡ�ô����ҵĸ������� ��
��2�������δ�������ǡ�ûص������еĸ��ʣ�
��3���������δ����������ڱ����ϵĸ��ʼ���P1�����ڶ����ϵĸ��ʼ���P2����P1�� P2������������������ߡ�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com