
【题目】近年来,琼海市在国际和国内的知名度越来越大,带动旅游事业蓬勃发展,吸引大批海内外游客前来观光旅游、购物度假,下面的图1和2分别反映了该市2011-2014年游客总人数和旅游业总收入情况.根据统计图提供的信息,解答下列问题:
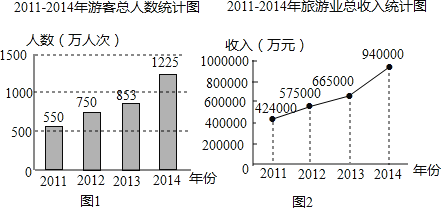
(1)2014年游客总人数为 万人次,旅游业总收入为 万元;
(2)在2012年,2013年,2014年这三年中,旅游业总收入增长幅度最大的是 年,这一年的旅游业总收入比上一年增长的百分率为 (精确到1%);
(3)据统计,2014年琼海共接待国内游客1200万人,人均消费约700元.求海外游客人均消费约多少元?(注:旅游收入=游客人数×游客的人均消费)
【答案】(1)1225,940000;(2)2014,41%;(3)海外游客的人均消费为4000元
【解析】
(1)观察图像可知:2014年游客总人数为1225万人次,旅游业总收入为940000万元; (2)在2012年,2013年,2014年这三年中,旅游业总收入增长幅度最大的是2014年,这一年比上一年增长的百分率为![]() ≈41%; (3)设海外游客的人均消费为
≈41%; (3)设海外游客的人均消费为![]() 元,根据题意,
元,根据题意,![]() 解得
解得![]() 的值即可.
的值即可.
(1)由图可知,2014年游客总人数为1225万人次,旅游业总收入为940000万元,
故答案为:1225;940000.
(2)在2012年,2013年,2014年这三年中,旅游业总收入增长幅度最大的是2014年,
这一年比上一年增长的百分率为![]() ≈41%,
≈41%,
故答案为:2014;41%;
(3)设海外游客的人均消费为![]() 元,根据题意得:
元,根据题意得:
![]()
解这个方程,得![]() .
.
答:海外游客的人均消费为4000元


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 与原点重合点
与原点重合点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.
轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;
(2)补全条形统计图,并计算阅读部分圆心角是 度.
(3)若该校九年级爱好阅读的学生有150人,估计九年级有 名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以斜边AB为直径作Rt△ABC的外接圆,圆心为O,P为弧BC的中点.
(1)只用直尺和笔作图:在弧ACB另一侧的圆上找一点G,连接PG交BC于点D,使D成为BC中点.并说明你的理由.
(2)在(1)小题图形基础上,在DG上取一点K,使DK=DP,连接CK、BK,判断四边形PBKC的形状,并证明你的结论.
(3)如题图2,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:当∠CAB=60°时,H为AB四等分点.
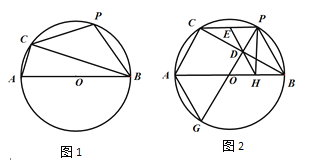
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.

(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是____________,位置关系是____________;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
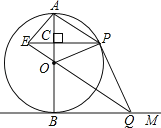
【题目】如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
(1)求证:△BOQ≌△POQ;
(2)若直径AB的长为12.
①当PE= 时,四边形BOPQ为正方形;
②当PE= 时,四边形AEOP为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线y=![]() (x>0)交于点A(1,a).
(x>0)交于点A(1,a).
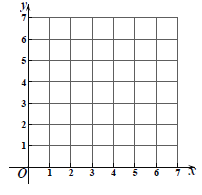
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n)(m>3)是直线l上一动点,过点P分别作x轴、y轴的平行线,交双曲线y=![]() (x>0)于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W.横、纵坐标都是整数的点叫做整点.
(x>0)于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W.横、纵坐标都是整数的点叫做整点.
①当m3 时,直接写出区域W 内的整点个数;
②若区域W 内有整点,且个数不超过 5 个,结合图象,求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
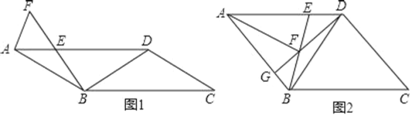
【题目】在ABCD中,连接对角线BD,AB=BD,E为线段AD上一点,AE=BE,F为射线BE上一点,DE=BF,连接AF.
(1)如图1,若∠BED=60°,CD=2![]() ,求EF的长;
,求EF的长;
(2)如图2,连接DF并延长交AB于点G,若AF=2DE,求证:DF=2GF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com