练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

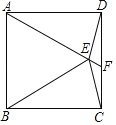
    【题目】如图，在正方形ABCD中，△ABE为等边三角形，连接DE，CE，延长AE交CD于F点，则∠DEF的度数为_____．

    【答案】105°

    【解析】

    根据四边形ABCD是正方形，可得AB=AD，∠BAD=90°，△ABC为等边三角形，可得AE=BE=AB，∠EAB=60°，从而AE=AD，∠EAD=30°，进而求得∠AED的度数，再根据平角定义即可求得∠DEF的度数．

    ∵四边形ABCD是正方形，

    ∴AB=AD，∠BAD=90°，

    ∵△ABE为等边三角形，

    ∴AE=BE=AB，∠EAB=60°，

    ∴AE=AD，

    ∠EAD=∠BAD﹣∠BAE=30°，

    ∴∠AED=∠ADE=（180°﹣30°）=75°，

    ∴∠DEF=180°﹣∠AED=180°﹣75°=105°．

    故答案为105°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一天，某交警巡逻车在东西方向的青年路上巡逻，他从岗亭出发，晚上停留在处.规定向东方向为正，向西方向为负，当天行驶情况记录如下（单位：千米）：

    +5，-8，+10，-12，+6，-18，+5，-2.

    （1）处在岗亭的什么方向？距离岗亭多远？

    （2）若巡逻车每行驶1千米耗油0.1升，这一天共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

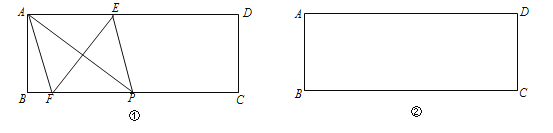
    【题目】如图，在矩形ABCD中，AB＝1，BC＝3．

    （1）在图①中，P是BC上一点，EF垂直平分AP，分别交AD、BC边于点E、F，求证：四边形AFPE是菱形；

    （2）在图②中利用直尺和圆规作出面积最大的菱形，使得菱形的四个顶点都在矩形ABCD的边上，并直接标出菱形的边长．（保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

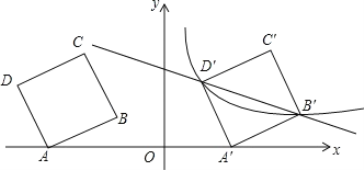
    【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(-6,0),D(-7,3)，点B、C在第二象限内．

    (1)点B的坐标 ；

    (2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；

    (3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在，请求出符合题意的点P、Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.

    例如: |6+7|=6+7 ； |6－7|=7－6 ； |7－6|=7－6 ； |－6－7|=6+7.

    （1）根据上面的规律,把下列各式写成去掉绝对值符号的形式:

    ①|7－21|=_____；②=_____；③=_____；④│a－b│=____（a<b）；

    （2）用合理的方法计算: .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】蜗牛从某点O开始沿东西方向直线爬行，规定向东爬行的路程记为正数，向西爬行的路程记为负数．爬行的各段路程依次为（单位：厘米）：.问：

    （1）蜗牛最后是否回到出发点O？

    （2）蜗牛离开出发点O最远是多少厘米？

    （3）在爬行过程中，如果每爬行1厘米奖励一粒芝麻，则蜗牛可得到多少粒芝麻？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△AEB中，∠AEB＝90°，以斜边AB为边向Rt△AEB形外作正方形ABCD，若正方形ABCD的对角线交于点O（如图1）．

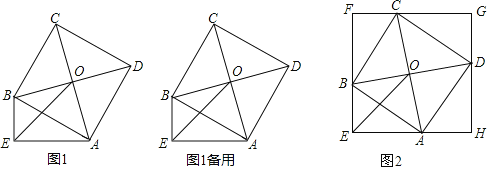
    （1）求证：EO平分∠AEB；

    （2）猜想线段OE与EB、EA之间的数量关系为　 　（直接写出结果，不要写出证明过程）；

    （3）过点C作CF⊥EB于F，过点D作DH⊥EA于H，CF和DH的反向延长线交于点G（如图2），求证：四边形EFGH为正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，如果直线 y＝kx 与函数 y＝的图象恰有 3 个不同的交点，则 k的取值范围是_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，点E为边BC的上一动点，作AF⊥DE交DE、DC分别于P、F点，连PC

    （1）若点E为BC的中点，求证：F点为DC的中点；

    （2）若点E为BC的中点，PE＝6，PC＝，求PF的长．

    查看答案和解析>>

    同步练习册答案